Collective models

Another, and actually older, way to look at nuclei is as a drop of “quantum fluid”. This ignores the fact that a nucleus is made up of protons and neutrons, and explains the structure of nuclei in terms of a continuous system, just as we normally ignore the individual particles that make up a fluid.

Equilibrium shape & deformation

Once we picture a nucleus as a fluid, we can ask question about its equilibrium shape. From experimental data we know that near closed shells nuclei are spherical, i.e., the equilibrium shape is a sphere. When both the proton and neutron number differ appreciably from the magic numbers, the ground state is often found to be axially deformed, either prolate (cigar like) or oblate (like a pancake). Since it is found that the nuclear fluid is to very good approximation incompressible, the dynamical excitations are those where the shape of the nucleus fluctuates, keeping the volume constant, as well as those where the nucleus rotates without changing its intrinsic shape.

Collective vibrations

Let us first look at collective vibrations, and for simplicity only at those of a spherical fluid drop. We can think of a large number of shapes; a complete set can be found by parametrising the surface as r = ∑ _L,Ma_LMY _LM(θ,ϕ), where Y _LM are the spherical harmonics and describe the multipolarity (angular momentum) of the surface. A few examples are shown in Figs. xxx, where we skecth the effects of monopole (L = 0), dipole (L = 1), quadrupole (L = 2) and octupole (L = 3) modes. Let us investigate these modes in turn, in the harmonic limit, where we look at small vibrations (small a_LM) only. Click here for a short movie.

Monopole

The monopole mode is the one where the size of the nuclear fluid oscillates, i.e., where the nucleus gets compressed. Experimentally one finds that the lowest excitation of this type, which in even-even nuclei carries the quantum number J^π = 0⁺, occurs at an energy of roughly

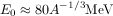
above the ground state. Compared to ordinary nuclear modes, which have energies of a few MeV, these are indeed high energy modes (15MeV for A = 216), showing the incompressibility of the nuclear fluid. Click here for a short movie.

Dipole

The dipole mode by itself is not very interesting: it corresponds to an overall translation of the centre of the nuclear fluid. One can, however, imagine a two-fuid model where a proton and neutron fluid oscillate against each other. This is a collective isovector (I=1) mode. It has quantum numbers J^π = 1⁻, occurs at an energy of roughly

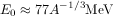
above the ground state, close to the monopole resonance. It shows that the neutron and proton fluids stick together quite strongly, and are hard to separate. Click here for a short movie.

Quadrupole

Quadrupole modes are the dominant vibrational feature in almost all nuclei. The very special properties of the lower multipolarities mean that these are the first modes available for low-energy excitations in nuclei. In almost all even-even nuclei we find a low-lying state (at excitation energy of less than 1 − 2MeV), which carries the quantum numbers J^π = 2⁺, and near closed shells we can often distinguish the second harmonic states as well (three states with quantum numbers J^π = 0⁺,2⁺,4⁺) .Click here for a short movie.

Octupole

Octupole modes, with J^π = 3⁻, can be seen in many nuclei. In nuclei where shell-structure makes quadrupole modes occur at very high energies, such as doubly magic nuclei, the octupole state is often the lowest excited state. Click here for a short movie.

Collective rotations

Once we have created a nucleus with axial deformation, i.e., a nucleus with ellipsoidal shape, but still axial symmetry about one axis, we can rotate the fluid around one of the non-symmetry axes to generate excitations. We cannot do it around a symmtery axis, since the resulting state would just be the same quantum state as we started with, and therefore the energy cannot change. A rotated state around a non-symmetry axis is a different quantum state, and therefore we can overlay many of these states, especially with constant rotational velocity. This is almost like the rotation of a dumbell, and we can predict the classical spectrum to be of the form

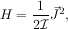
where 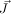is the classical angular momentum. We predict a quantum mechanical spectrum of the form

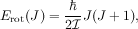
where J is now the angular momentum quantum number. Naively we expect the spectrum to be more compressed (the moment of inertial is larger) the more elongated the nucleus becomes. It is known that certain structures in nuclei indeed describe well deformed nuclei, up to super and hyper deformed (axis ratio from 1 : 1.2 to 1 : 2). Click here for a short movie.