5.4 Barrier penetration

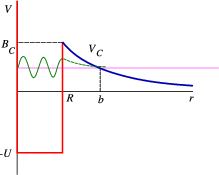
In order to understand quantum mechanical tunnelling in fission it makes sense to look at the simplest fission process: the emission of a He nucleus, so called $\alpha$ radiation. The picture is as in Fig.  5.12 .

---

---

Suppose there exists an $\alpha$ particle inside a nucleus at an (unbound) energy $>0$. Since it isn’t bound, why doesn’t it decay immediately? This must be tunnelling. In the sketch above we have once again shown the nuclear binding potential as a square well, but we have included the Coulomb tail,

$$V_{\text{Coulomb}}\left(r\right)=\frac{\left(Z-2\right)2e^2}{4\pi {𝜖}_{0}r}.$$

(5.20)

. The height of the barrier is exactly the coulomb potential at the boundary, which is the nuclear radius, $R_C=1.2A^{1.3}\text{ fm}$, and thus $B_C=2.4\left(Z-2\right)A^{-1∕3}$. The decay probability across a barrier can be given by the simple integral expression $P=e^{-2\gamma }$, with

$$\begin{array}{rcll}\gamma & =& \frac{{\left(2{\mu }_{\alpha }\right)}^{1∕2}}{\hslash }{\int \; <!--nolimits-->}_{R_C}^b{\left[V\left(r\right)-E_{\alpha }\right]}^{1∕2}dr& \\ & =& \frac{{\left(2{\mu }_{\alpha }\right)}^{1∕2}}{\hslash }{\int \; <!--nolimits-->}_{R_C}^b{\left[\frac{2\left(Z-2\right)e^2}{4\pi {𝜖}_{0}r}-E_{\alpha }\right]}^{1∕2}dr& \\ & =& \frac{2\left(Z-2\right)e^2}{2\pi {𝜖}_0\hslash v}\left[arccos\left(E_{\alpha }∕B_C\right)-\left(E_{\alpha }∕B_C\right)\left(1-E_{\alpha }∕B_C\right)\right],& \text{(5.21)}\end{array}$$

(here $v$ is the velocity associated with $E_{\alpha }$). In the limit that $B_C\gg E_{\alpha }$ we find

$$P=exp\left[-\frac{2\left(Z-2\right)e^2}{2{𝜖}_0\hslash v}\right].$$

(5.22)

This shows how sensitive the probability is to $Z$ and $v$!

This work is a UK OER project as part of the Skills for Scientists project. Please contact Niels Walet for more information

This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 2.0 Generic License