[back][up]

4.3 Time-dependent wave equation

In electromagnetism, you may have met the equations for the scalar potential Φ and vector potential A, which in free space are of the form

□Φ = 0,\qquad □A = 0,\qquad \text{where }□ = {1\over { c}^{2}} {{∂}^{2}\over ∂{t}^{2}} −{\mathop{∇}}^{2}.

These equation are satisfied for the “gauge choice” \mathop{∇}⋅A = 0, the Coulomb or radiation gauge.

As usual we can analyse what happens with external charge and current distributions, where the potentials satisfy

□Φ = {ρ(r,t)\over {ϵ}_{0}} ,\qquad □A = {μ}_{0}j(r,t).
(4.14)

Since we would like to know what happens for arbitrary sources, we are immediately led to the study of the Green function for the D’Alembertian or wave operator □,

□G(r,t;r',t) = δ(r −r')δ(t − t').

The boundary conditions are

  1. that the potentials should go to zero far from sources, G(r,t;r',t) → 0 as r →∞.
  2. that the effect of a source always occurs after its cause (causality) G(r,t;r',t) = 0 if t < t'.

For Galilean invariant problems, where we are free to change our origin in space and time, it is simple to show that the Green function only depends on (r −r') and t − t' ,

G(r,t;r',t) = G(r −r',t − t')\quad .

To obtain the functional form of G it is enough to solve for r' = 0, t' = 0, i.e.

\left ( {1\over { c}^{2}} {{∂}^{2}\over ∂{t}^{2}} −{\mathop{∇}}^{2}\right )G(r,t) = δ(r)δ(t).
(4.15)

4.3.1 Solution for the Green function by Fourier transforms

This standard method for time dependent wave equations is in several steps: First define the Fourier transform of G

It is easier to use the asymmetric definition of the Fourier and inverse Fourier transform, so that is what we shall use here.
\begin{eqnarray} \tilde{G}(k,ω)& =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {d}^{3}r\kern 1.66702pt \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits dt\kern 1.66702pt G(r,t)\mathop{exp}\nolimits [−i(k ⋅r − ωt)]\quad , %& \\ G(r,t)& =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {{d}^{3}k\over { (2π)}^{3}}\kern 1.66702pt \mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {dω\over 2π}\kern 1.66702pt \tilde{G}(k,ω)\mathop{exp}\nolimits [i(k ⋅r − ωt)]\quad ,%&(4.16) \\ δ(r)δ(t)& =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {{d}^{3}k\over { (2π)}^{3}}\kern 1.66702pt \mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {dω\over 2π}\kern 1.66702pt \mathop{exp}\nolimits [i(k ⋅r − ωt)]\quad , %& \\ \end{eqnarray}

and solve for the Fourier transform \tilde{G}(k,ω) by substituting the second of these relations into Eq. (4.15): This equation becomes

\eqalignno{ \left ( {1\over { c}^{2}} {{∂}^{2}\over ∂{t}^{2}} −{\mathop{∇}}^{2}\right )G(r,t) & =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {{d}^{3}k\over { (2π)}^{3}}\kern 1.66702pt \mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {dω\over 2π}\kern 1.66702pt \tilde{G}(k,ω)\left (−{{ω}^{2}\over {c}^{2}} + {k}^{2}\right )\mathop{exp}\nolimits [i(k ⋅r − ωt)] & & \cr & =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {{d}^{3}k\over { (2π)}^{3}}\kern 1.66702pt \mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {dω\over 2π}\kern 1.66702pt \mathop{exp}\nolimits [i(k ⋅r − ωt)]\quad . & & }

If we now equate the integrands, we find that

\eqalignno{ \tilde{G}(k,ω)\left (−{{ω}^{2}\over {c}^{2}} + {k}^{2}\right ) = 1\quad , & & \cr \tilde{G}(k,ω) = {−{c}^{2}\over { ω}^{2} − {c}^{2}{k}^{2}}\quad . & & }

We now substitute \tilde{G}(k,ω) back into (4.16)

G(r,t) = −{c}^{2}\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {{d}^{3}k\over { (2π)}^{3}}\kern 1.66702pt \mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {dω\over 2π}\kern 1.66702pt {\mathop{exp}\nolimits [i(k ⋅r − ωt)]\over {ω}^{2} − {c}^{2}{k}^{2}} \quad .
(4.17)

Integration over Euler angles

The {d}^{3}k part of the integral (4.17) is of the generic form

I =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {d}^{3}k\kern 1.66702pt {e}^{ik⋅r}f({k}^{2})

Integrals of this type can be dealt with in a standard way: We are free to choose the {k}_{3} axis to our benefit, since we integrate over all k, and this preferred direction makes no difference to the value of the integral. Thus, we choose the {k}_{3}-axis parallel to r, and find

\begin{eqnarray*} I& =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {k}^{2}dk\kern 1.66702pt \mathop{sin}\nolimits θdθ\kern 1.66702pt dϕ\kern 1.66702pt {e}^{ikr\mathop{ cos}\nolimits θ}f({k}^{2}) %& \\ & =& 2π{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{k}^{2}dk\kern 1.66702pt {\left [{−{e}^{ikr\mathop{ cos}\nolimits θ}\over ikr} \right ]}_{0}^{π}f({k}^{2})%& \\ & =& 2π{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{kdk\over ir} \kern 1.66702pt \left [{e}^{ikr} − {e}^{−ikr}\right ]f({k}^{2}) %& \\ & =& 2π{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{kdk\over ir} {e}^{ikr}f({k}^{2})\quad . %& \\ \end{eqnarray*}

Note the trick used to transform the penultimate line into the last one: we change the second term in square brackets into an integral over (−∞,0].

We can now apply this simplification to (4.17) to find

G(r,t) = − {{c}^{2}\over { (2π)}^{2}ir}{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}kdk\kern 1.66702pt {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{dω\over 2π}\kern 1.66702pt {\mathop{exp}\nolimits [i(kr − ωt)]\over {ω}^{2} − {c}^{2}{k}^{2}} .
(4.18)

We now tackle the ω integral,

{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{dω\over 2π}\kern 1.66702pt {{e}^{−iωt}\over { ω}^{2} − {c}^{2}{k}^{2}}.
(4.19)

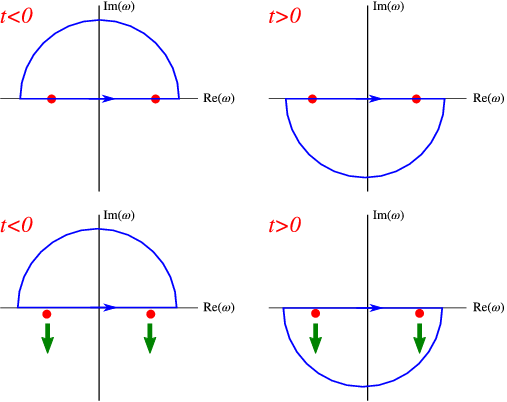
The problem with this integrand is that we have poles at ω = ±ck on the real axis, and we have to integrand around these in some way. Here the boundary conditions enter. We shall use contour integration by closing off the integration contour by a semicircle in the complex ω plane. The position of the semicircle will be different for positive and negative t: Look at

ω = R{e}^{iϕ},

where R is the radius of the semicircle (which we shall take to infinity), and ϕ is the variable that describes the movement along the semicircle. We find that

\mathop{exp}\nolimits [−iωt] =\mathop{ exp}\nolimits [−iRt\mathop{cos}\nolimits ϕ]\mathop{exp}\nolimits [Rt\mathop{sin}\nolimits ϕ].

Since we want to add a semicircle without changing the integral, we must require that

\mathop{exp}\nolimits [Rt\mathop{sin}\nolimits ϕ] → 0\text{ as }R →∞,

so that no contribution is made to the integral. This occurs if t\mathop{sin}\nolimits ϕ < 0. Thus, if t < 0, we close the contour in the upper half plane, and if t > 0 in the lower one, see Fig. 4.2.

contour

Figure 4.2: The contours used in the ω integral (4.19).

Now we have turned our ω integral into a contour integral, we need to decide how to deal with the poles, which lie on the real acis. Our time boundary condition (causality) states that G = 0 if t < 0, and thus we want to move the poles to just below the contour, as in the second part of Fig. 4.2, or by shifting the integration up by an infinitesimal amount above the real axis (these two ways of doing the integral are equivalent). The integral for t > 0 can then be done by residues, since we have two poles inside a closed contour. Note that the orientation of the contour is clockwise, and we just have a minus sign in the residue theorem,

{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{dω\over 2π}\kern 1.66702pt {{e}^{−iωt}\over { ω}^{2} − {c}^{2}{k}^{2}} = \mathop{∮ }\nolimits {dz\over 2π}\kern 1.66702pt {{e}^{−izt}\over (z − ck)(z + ck)} = −2πi({R}_{+} + {R}_{−})\quad .

Here {R}_{±} is the residue of the poles (the “strength” of the pole),

{R}_{+} = {1\over 2π} {{e}^{−ickt}\over 2ck} ,\qquad {R}_{−} = {1\over 2π} {{e}^{+ickt}\over −2ck} ,

and we thus find that

{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{dω\over 2π}\kern 1.66702pt {{e}^{−iωt}\over { ω}^{2} − {c}^{2}{k}^{2}} = − {i\over 2ck}\left ({e}^{−ickt} − {e}^{ickt}\right ).

If we substitute this into (4.18), we find that (t > 0!)

\begin{eqnarray*} G(r,t)& =& {c\over { (2π)}^{2}2r}{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}dk\left ({e}^{ik(r−ct)} − {e}^{ik(r+ct)}\right )%& \\ & =& {c\over 4πr}\left (δ(r − ct) − δ(r + ct)\right ) %& \\ & =& {c\over 4πr}δ(r − ct). %& \\ \end{eqnarray*}

We discard the second delta function above, since its argument r + ct > 0 if t > 0, and thus the δ function is always zero.

If we now reinstate t' and r' using Galilean invariance, we find that

G(r,t;r',t) = {c\over 4π|r −r'|}δ{\bigl (|r −r'|− c(t − t')\bigr )}.
(4.20)

For reasons that will become clear below, this is called the retarded Green function. It vanishes everywhere except on the backward light cone, |r −r'| = c(t − t'), see Fig. 4.3.

lightcone1

Figure 4.3: The backward light cone starting from r,t

Two special cases can be obtained simply:

  1. For a static charge distribution (and no current), we find
    \begin{eqnarray*} Φ(x)& =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {d}^{3}r'dt' {c\over 4π|r −r'|}δ\left (|r −r'|− c(t − t')\right ){ρ(r')\over {ϵ}_{0}} %& \\ & =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {d}^{3}r' {1\over 4π{ϵ}_{0}|r −r'|}{ρ(r')\over {ϵ}_{0}} , %& \\ \end{eqnarray*}

    using

    \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits dt'δ\left (|r −r'|− c(t − t')\right ) = {1\over c}.

  2. If ρ(r',t') describes a single moving charged particle, which is at a position s(t') at time t', we use ρ = qδ(r'−s(t')) and we find the Liénard-Wiechert potential,
    \begin{eqnarray*} Φ(x,t)& =& \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {d}^{3}r'dt' {c\over 4π|r −r'|}δ\left (|r −r'|− c(t − t')\right )qδ(r'−s(t'))∕{ϵ}_{0}%& \\ & =& q∕{ϵ}_{0}\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits dt' {c\over 4π|r −s(t')|}δ\left (|r −s(t')|− c(t − t')\right ). %& \\ \end{eqnarray*}

The δ function selects those points on the path followed by the charge that intersect the light-cone with apex r,t at a time s(t'),t'.

4.3.2 Wave equations in (2 + 1) dimensions

Green functions for wave equations in (2+1) dimensions can be solved directly by the Fourier transform method, or, if you know the result in (3+1) dimensions, they can also be obtained by “integrating out” the extra dimensions:

{G}^{(2)}(x − x',y − y',t − t') =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits dz'\kern 1.66702pt G(r,t;r',t')
(4.21)

for t > t'.

This can be checked quite simply. From

□G(r,t;r',t) = δ(r −r')δ(t − t').

We find that

\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits dz'\kern 1.66702pt □G(r,t;r',t') =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits dz'\kern 1.66702pt δ(r −r')δ(t − t').

If we now swap differentiation and integration, we get

□\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits dz'\kern 1.66702pt G(r,t;r',t') = δ(x − x')δ(y − y')δ(t − t').

Since \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits dz'\kern 1.66702pt G(r,t;r',t') = {G}^{(2)}(x − x',y − y',t − t') is independent of z, we find that {∂}_{z}^{2}{G}^{(2)} = 0, and thus {G}^{(2)} is indeed the Green function for the two-dimensional wave equation.

From equation (4.20) we find

\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits dz'\kern 1.66702pt {c\over 4π|r −r'|}δ{\bigl (|r −r'|− c(t − t')\bigr )}

Integrate using the delta function, which is nonzero at {z'}_{±} = z ±\sqrt{{c}^{2 } {(t − t')}^{2 } − {(x − x')}^{2 } − {(y − y')}^{2}}, and thus

δ{\bigl (|r −r'|− c(t − t')\bigr )} = {|z − z'|\over \sqrt{{c}^{2 } {(t − t')}^{2 } − {(x − x')}^{2 } − {(y − y')}^{2}}}{ \mathop{∑ }}_{α=±}δ(z' − {z'}_{±})\quad .

Both poles give the same contribution, and the retarded Green function is thus

{G}^{(2)}(x−x',t − t') = {c\over 2π} {1\over { ({c}^{2}{(t − t')}^{2} −|x−x'{|}^{2})}^{1∕2}}
(4.22)

for t > t' , where x is a 2-dimensional space vector x = (x,y). In contrast to the 3+1 case, this is non-vanishing in the whole of the backward light-cone, not just on it!

[back][up]