5.3 Special cases with examples: first integrals

Let us look at a few special cases for the functional I defined in (5.1).

5.3.1 Functional of first derivative only

We first consider the case F(y(x),y'(x),x) = F(y'(x),x), and thus independent of y. The Euler-Lagrange equation,

has the simple solution

This equation is called the “first integral” of the problem.

Figure 5.1: The distance between two points along a path connecting two fixed points

Example 5.2: 

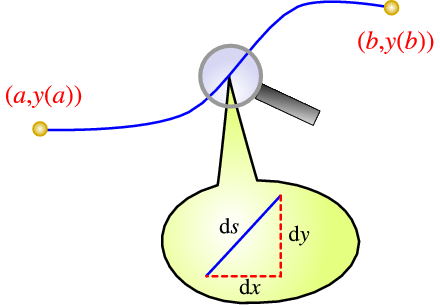
Show that the shortest distance between any two fixed points (in 2D space, for simplicity) is along a straight line.

Solution: 

We parametrise the curve connecting the two points by (x,y(x)) (which assumes each value x only occurs once, and we thus only look at a–sensible–subclass of paths). The endpoints (a,y(a)) and (b,y(b)) are fixed. If we take a small step along the line, the distance travelled is

{(ds)}^{2} = {(dx)}^{2} + {(dy)}^{2} = {(dx)}^{2}[1 + {(dy∕dx)}^{2}].

Thus

ds = {(1 +{ y'}^{2})}^{1∕2}dx.

The total path length is thus the functional

L[y] ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{a}^{b}{(1 +{ y'}^{2})}^{1∕2}dx,

which is of the form investigated above. Thus

{∂F\over ∂y'(x)} = {y'(x)\over { (1 +{ y'(x)}^{2})}^{1∕2}} = k.

It is not too hard to solve this equation, by squaring both sides,

\eqalignno{ {y'}^{2}(x) & = {k}^{2}(1 +{ y'(x)}^{2})\quad , & & \cr y'(x) & = {k\over \sqrt{1 − {k}^{2}}} = c\quad , & & \cr y(x) & = cx + d & & }

We can determine c and d from the boundary conditions

\eqalignno{ c & = {y(b) − y(a)\over b − a} , & & \cr d & = {by(a) − ay(b)\over b − a} . & & }

5.3.2 No explicit dependence on x

If F(y,y',x) = F(y,y'), independent of x, we proceed in a slightly different way. We combine the Euler-Lagrange equation

with an explicit differentiation of F,

to find

Combining left-hand and right-hand sides, we find

We thus conclude that for F[y,y'] (i.e., no explicit x dependence in the functional) we have the first integral

Figure 5.2: Snell’s law

Example 5.3: 

Fermat’s principle of geometrical optics states that light always travels between two points along the path that takes least time, or equivalently which has shortest optical path length (since time is pathlength divided by the speed of light). Show that this implies Snell’s law.

Solution: 

Following notations as for the shortest path problem above, we find that the travel time of light along an arbitrary path y(x) is

\eqalignno{ t[y] & =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits {ds\over v} & & \cr & = {1\over c}\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits n(x,y)ds & & \cr & = {1\over c}\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits n(y)\sqrt{1 +{ y' }^{2}}dx, & & }

or in terms of the optical path

p[y] =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits n(y)\sqrt{1 +{ y' }^{2}}dx.

We have assumed that n(x,y) = n(y). Its correctness depends on both path and arrangement of the problem.

We now use the result (5.5) from above, and find with F = n(y(x))\sqrt{1 +{ y' }^{2}} that

\eqalignno{ \text{constant} & = n(y)\sqrt{1 +{ y' }^{2}} − y' {n(y)y'\over \sqrt{1 +{ y' }^{2}}} & & \cr & = n(y)\left ( {1 +{ y'}^{2}\over \sqrt{1 +{ y' }^{2}}} − {{y'}^{2}\over \sqrt{1 +{ y' }^{2}}}\right ) & & \cr & = n(y) {1\over \sqrt{1 +{ y' }^{2}}}\quad . & & }

Thus

\class{boxed}{n(y) = \text{const}\sqrt{1 +{ y' }^{2}}\quad . }

(5.6)

Now consider areas where n(y) is constant. The problem turns into the least distance problem discussed above, and we find that in such an area the optical path becomes a straight line. We now assume two such areas, with index of refraction {n}_{1} below the x axis, and {n}_{2} above, see Fig. 5.2. As usual it is easy to see that y'(x) =\mathop{ tan}\nolimits ϕ, and from

\sqrt{1 +{ y' }^{2}} = \sqrt{1 +{\mathop{ tan} \nolimits }^{2 } ϕ} =\mathop{ sec}\nolimits ϕ = 1∕\mathop{cos}\nolimits ϕ

we conclude from Eq. (5.6) that n\mathop{cos}\nolimits ϕ = \text{constant}. Thus

{n}_{1}\mathop{ cos}\nolimits {ϕ}_{1} = {n}_{2}\mathop{ cos}\nolimits {ϕ}_{2}\quad ,

and using \mathop{cos}\nolimits ϕ =\mathop{ cos}\nolimits ({π\over 2} − θ) =\mathop{ sin}\nolimits θ we get

\class{boxed}{{n}_{1}\mathop{ sin}\nolimits {θ}_{1} = {n}_{2}\mathop{ sin}\nolimits {θ}_{2}, }

i.e., we have proven Snell’s law.

Let’s look at one more related problem

Example 5.4: 

The brachistochrone is the curve along with a particle slides the fastest between two points under the influence of gravity; think of a bead moving along a metal wire. Given two fixed endpoints, A = (0,0) and a second point B, find the brachistichrone connecting these points.

Solution: 

We find for the travel time

T ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{A}^{B}dt ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{A}^{B} {dt\over ds}ds ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{A}^{B}{ds\over v} ,

which has to be a minimum. From energy conservation we get

{1\over 2}m{v}^{2} = mgy,\text{ or }v = \sqrt{2gy},

and as before

ds = \sqrt{1 +{ y' }^{2}}dx\quad .

Taking all of this together

T[y] ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{b}{\left ({1 +{ y'}^{2}\over 2gy} \right )}^{1∕2}dx.

(5.7)

We now drop the factor 2g from the denominator, and minimise

I[y] ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{b}{\left ({1 +{ y'}^{2}\over y} \right )}^{1∕2}dx.

Since F ={ \left ({1+{y'}^{2}\over y} \right )}^{1∕2} has no explicit x dependence, we find

F −{∂F\over ∂y'} y' = \text{constant},

i.e.,

\eqalignno{ \text{const} & = {1 +{ y'}^{2}\over y} − {1\over \sqrt{y}} {y'\over \sqrt{1 +{ y' }^{2}}y'} & & \cr & = {1 +{ y'}^{2}\over \sqrt{y(1 +{ y' }^{2 } )}} − {{y'}^{2}\over \sqrt{y(1 +{ y' }^{2 } )}} & & \cr & = {1\over \sqrt{y(1 +{ y' }^{2 } )}}\quad . & & }

Substituting a convenient value for the constant, we find

\class{boxed}{y(1 +{ y'}^{2}) = 2R, }

which is the equation for a cycloid. To solve this, we write y' =\mathop{ cot}\nolimits (ϕ∕2), which now leads to

1 +{ y'}^{2} = 1 +{\mathop{ cos}\nolimits }^{2}(ϕ∕2)∕{\mathop{sin}\nolimits }^{2}(ϕ∕2) = 1∕{\mathop{sin}\nolimits }^{2}(ϕ∕2),

and

y(ϕ) = 2R∕(1 +{ y'}^{2}) = 2R{\mathop{sin}\nolimits }^{2}(ϕ∕2) = R(1 −\mathop{ cos}\nolimits ϕ).

(5.8)

That would be fine if we knew also x(ϕ), so we can represent the curve by a parametric plot! We have from (5.8)

{dx\over dϕ} = {1\over dy∕dx} {dy\over dϕ} =\mathop{ tan}\nolimits (ϕ∕2)2R\mathop{sin}\nolimits ϕ∕2\mathop{cos}\nolimits ϕ∕2 = 2R{\mathop{sin}\nolimits }^{2}ϕ∕2 = y.

Thus using Eq. (5.8) we get x = R(ϕ −\mathop{ sin}\nolimits ϕ) + C. Imposing the condition that the curve runs through (0,0), we find

\class{boxed}{x = R(ϕ −\mathop{ sin}\nolimits ϕ),\qquad y = R(1 −\mathop{ cos}\nolimits ϕ). }

We determine R and an angle {ϕ}_{0} from the conditions

(R({ϕ}_{0} −\mathop{ sin}\nolimits {ϕ}_{0}),R(1 −\mathop{ cos}\nolimits {ϕ}_{0})) = (b,y(b)).

This has multiple solutions. In order to cover all points with positive x∕y once, we need to require 0 < ϕ < 2π, see Fig. 5.3.

---

Figure 5.3: x∕y as a function of {ϕ}_{0}.

---

Once we have fixed the range of ϕ, we can then solve for the brachystochrone, see Fig. 5.4 for a few examples.

---

Figure 5.4: A few brachystochrone curves for {y}_{f} = 1.

---

So what is the value of the travel time? Substituting the solution into Eq. (5.7) we get

\eqalignno{ T & ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{{ϕ}_{0} }{\left ( {2R\over 2g{y}^{2}}\right )}^{1∕2}ydϕ & & \cr & = {ϕ}_{0}\sqrt{{R\over g}} \quad . & & }