[forward][back][up]

A.2 Contour Integration

Let us look at the effects of integrating the powers of z along a line in the complex plane (note that we implicitely assume that the answer is independent of the position of the line, and only depends on beginning and end!)

{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{{z}_{0}}^{{z}_{1} }{z}^{n}\kern 1.66702pt dz,\quad n ∈ ℤ.
(A.3)

We know how to integrate powers, so apart from the case n = −1, we get

\eqalignno{ {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{{z}_{0}}^{{z}_{1} }{z}^{n}\kern 1.66702pt dz & ={ \left [ {1\over n + 1}{z}^{n+1}\right ]}_{{ z}_{0}}^{{z}_{1} },\quad n\mathrel{≠} − 1, &\text{(A.4)} \cr {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{{z}_{0}}^{{z}_{1} }{z}^{−1}\kern 1.66702pt dz & ={ \left [\mathop{log}\nolimits z\right ]}_{{ z}_{0}}^{{z}_{1} },\quad n = −1. &\text{(A.5)} }

So the first of these integrals is indepdent of the path between begin and end. It thus goes to zero as we look at a closed path, but the second integral actually does depend on the path of integration:

\text{Use }z = r{e}^{iϕ};\mathop{log}\nolimits (z) =\mathop{ log}\nolimits (r) + iϕ.
(A.6)

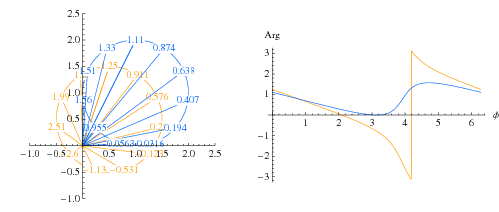
We have two options: the contour (the technical word for the closed path) either encloses the origin where the singularity resides or not, see Fig. A.1.

Contourill1

Figure A.1: Two contours: The blue one does not include the origin, the orange one does. The numbers on the left plot show the phase of the relevant complex numbers. These are also graphed in the right panel.

As we move the around the curve, you notice for the blue curve that the phase (the number plotted on the line connecting to the point for which we calculate the phase) gently oscillates up and down, and thus the answer of the contour integral is zero; for the orange curve we see a jump at the negative x-axis. This is due to a convention; in principle we can put this jump along any half-line in the complex plane ending at the origin.
If we move the value at the right of the jump down by 2π (making the function continuous) we realise that the begin and endpoint differ in phase by 2π. Thus for any contour enclosing the origin the phase changes by 2π, and thus we expect that

\mathop{∮ }\nolimits {z}^{−1}dz = ±2πi
(A.7)

for a contour enclosing the origin. The sign is positive if we integrate around in the positive sense (anti-clockwise), and negative if we do the integral along a contour that encircles the origin in a clockwise fashion.

If a function f(z) behaves like {1\over z−c} near the point c, we say that the function has a pole at z = c.

[forward][back][up]