[forward][up]

3.1 Linear operators

A linear operator L acts on vectors a,b\mathop{\mathop{…}} in a linear vector space V to give new vectors La, Lb,\mathop{\mathop{…}} such that1

L(λa + μb) = λLa + μLb

Example 3.1: 

  1. Matrix multiplication of a column vector by a fixed matrix is a linear operation, e.g.
    Lx = \left (\array{ 1&2& 3\cr 4&8 &−1} \right )x.
  2. Differentiation is a linear operation, e.g.,
    Lf(x) = {d\over dx}f(x).
  3. Integration is linear as well,
    \eqalignno{ ({L}_{1}f)(x) & ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{x}f(x')dx', & & \cr ({L}_{2}f)(x) & ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}G(x,x')f(x')dx', & & }

    are both linear (see example sheet).

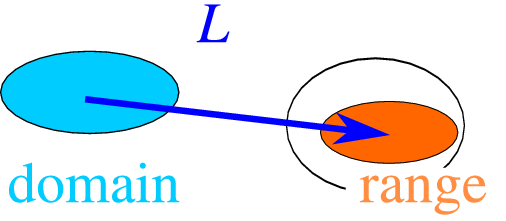
3.1.1 Domain, Codomain and Range

If the operators L maps the vector f on the vector g, Lf = g, the vector space of f’s (the domain) can be different from the vector space of g’s (the codomain or target). L is an operator which maps the domain onto the codomain, and even though it is defined for every element of the domain, the image of the domain (called the “range of L” or the “image of L”) is in general only a subset of the codomain, see Fig. 3.1, even though in many physical cases we shall assume that the range and codomain coincide.

domain

Figure 3.1: The definition of domain, codomain and range

Example 3.2: 

  1. The operator L: {ℂ}^{n} → ℂ defined by La = (a,b) with b a fixed vector, is a linear operator.
  2. The matrix \left (\array{ 3&2&1\cr 6&4 &2} \right ) maps from the space {ℝ}^{3} of 3-vectors to the codomain {ℝ}^{2} of 2-vectors. The range is the 1D subset of vectors λ\left (\array{ 1\cr 2} \right ), λ ∈ ℝ.
  3. The (3D) gradient operator \mathop{∇} maps from the space of scalar fields (f(x) is a real function of 3 variables) to the space of vector fields (\mathop{∇}f(x) is a real 3-component vector function of 3 variables).

3.1.2 Matrix representations of linear operators

Let L be a linear operator, and y = lx. Let {e}_{1}, {e}_{2}, …and {u}_{1}, {u}_{2}, …be chosen sets of basis vectors in the domain and codomain, respectively, so that

x ={ \mathop{∑ }}_{i}{e}_{i}{x}_{i},\qquad y ={ \mathop{∑ }}_{i}{u}_{i}{y}_{i}.

Then the components are related by the matrix relation

{y}_{j} ={ \mathop{∑ }}_{i}{L}_{ji}{x}_{i},

where the matrix {L}_{ji} is defined by

L{e}_{i} ={ \mathop{∑ }}_{j}{u}_{j}{L}_{ji} ={ \mathop{∑ }}_{j}{\left ({L}^{T}\right )}_{ ij}{u}_{j}.
(3.1)

Notice that the transformation relating the components x and y is the transpose of the matrix that connects the basis. This difference is related to what is sometimes called the active or passive view of transformations: in the active view, the components change, and the basis remains the same. In the passive view, the components remain the same but the basis changes. Both views represent the same transformatio!

If the two basis sets \{{e}_{i}\} and \{{u}_{j}\} are both orthonormal, we can find the matrix elements of L as an innerproduct,
{L}_{ji} = ({u}_{j},L{e}_{i}).
(3.2)

Example 3.3: 

Find a matrix representation of the differential operator {d\over dx} in the space of functions on the interval (−π,π).

Solution: 

Since domain and codomain coincide, the bases in both spaces are identical; the easiest and most natural choice is the discrete Fourier basis 1,\{\mathop{cos}\nolimits nx,\mathop{sin}\nolimits nx{\}}_{n=1}^{∞}. With this choice, using (\mathop{cos}\nolimits nx)' = −n\mathop{sin}\nolimits nx and (\mathop{sin}\nolimits nx)' = n\mathop{cos}\nolimits nx, we find

{d\over dx}\left (\array{ 1\cr \mathop{cos}\nolimits x \cr \mathop{sin}\nolimits x\cr \mathop{cos} \nolimits 2x \cr \mathop{sin}\nolimits 2x\cr \mathop{\mathop{⋮}} } \right ) = \left (\array{ 0\cr −\mathop{ sin}\nolimits x \cr \mathop{cos}\nolimits x\cr −2\mathop{ sin} \nolimits 2x \cr 2\mathop{cos}\nolimits 2x\cr \mathop{\mathop{⋮}} } \right ) = {M}^{T}\left (\array{ 1\cr \mathop{cos}\nolimits x \cr \mathop{sin}\nolimits x\cr \mathop{cos} \nolimits 2x \cr \mathop{sin}\nolimits 2x\cr \mathop{\mathop{⋮}} } \right )\quad .

We can immediately see that the matrix representation ”M” takes the form

{ M}^{T} = \left (\array{ 0&0& 0 &0& 0 &\mathop{\mathop{…}}\cr 0&0 &−1 &0 & 0 & \cr \ 0&1& 0 &0& 0 &\cr 0&0 & 0 &0 &−2& \cr 0&0& 0 &2& 0 &\cr \mathop{\mathop{⋮}}& & & && &\mathrel{⋱} } \right )\quad .

Matrix representation of the time-independent Schrödinger equation

Another common example is the matrix representation of the Schrödinger equation. Suppose we are given an orthonormal basis \{{ϕ}_{i}{\}}_{i=1}^{∞} for the Hilbert space in which the operator \hat{H} acts. By decomposing an eigenstate ψ of the Schrödinger equation,

\hat{H}ψ(x) = Eψ(x)

in the basis {ϕ}_{j}(x) as ψ ={\mathop{ \mathop{∑ }}\nolimits }_{j}{c}_{j}{ϕ}_{j}, we get the matrix form

{\mathop{∑ }}_{j}{H}_{ij}{c}_{j} = E{c}_{i}\quad ,
(3.3)

with

{H}_{ij} = ({ϕ}_{i},\hat{H}{ϕ}_{j}) =\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits dx\kern 1.66702pt {ϕ}_{i}{(x)}^{∗}H{ϕ}_{ j}(x)\quad .

This is clearly a form of Eq. (3.2).

The result in Eq. (3.3) is obviously an infinite-dimensional matrix problem, and no easier to solve than the original problem. Suppose, however, that we truncate both the sum over j and the set of coefficients c to contain only N terms. This can then be used to find an approximation to the eigenvalues and eigenvectors. See the Mathematica notebook heisenberg.nb for an example how to apply this to real problems.

3.1.3 Adjoint operator and hermitian operators

You should be familiar with the Hermitian conjugate (also called adjoint) of a matrix, the generalisation of transpose: The Hermitian conjugate of a matrix is the complex conjugate of its transpose,

{({M}^{†})}_{ ij} = {({M}_{ji})}^{∗},\quad \text{or}\quad {M}^{†} = {({M}^{T})}^{∗}.

Thus

{ \left (\array{ 0&i\cr i&0 } \right )}^{†} = \left (\array{ 0 &−i \cr −i& 0 } \right ),\qquad {\left (\array{ 0 &i\cr −i &0 } \right )}^{†} = \left (\array{ 0 &i \cr −i&0 } \right ).

We can also define the Hermitian conjugate of a column vector, if
v = \left (\array{ {v}_{1} \cr \mathop{\mathop{⋮}}\cr {v}_{ n} } \right ),\quad {v}^{†} = ({v}_{ 1}^{∗},\mathop{\mathop{…}},{v}_{ n}^{∗}).

This allows us to write the inner product as a matrix product,

(w,v) ={ w}^{†}v.

The most useful definition of Hermitian conjugate, which will be generalised below, is through the inner product:

The hermitian conjugate {M}^{†} of a matrix M has the property that for any two vectors a and b in the range and domain,
(a,Mb) = ({M}^{†}a,b).

Thus, with a little algebra,
(a,Mb) ={ \mathop{∑ }}_{ij}{a}_{i}^{∗}{M}_{ ij}{b}_{j} ={ \mathop{∑ }}_{ij}{a}_{i}^{∗}{({M}_{ ji}^{†})}^{∗}{b}_{ j} ={ \mathop{∑ }}_{ij}{({M}_{ji}^{†}{a}_{ i})}^{∗}{b}_{ j} = ({M}^{†}a,b),
(3.4)

see Fig. 3.2.

hermit1

Figure 3.2: The definition of a matrix and its Hermitian conjugate

From the examples above, and the definition, we conclude that if M is an m × n matrix, {M}^{†} is an n × m one.

We now use our result (3.4) above for an operator, and define

\mathop{∀}a ∈\text{codomain},b ∈\text{domain} : \quad (a,Lb) = ({L}^{†}a,b) = {(b,{L}^{†}a)}^{∗}

where the last two terms are identical, as follows from the basic properties of the scalar product, Eq. (2.2). A linear operator L maps the domain onto the codomain; its adjoint {L}^{†} maps the codomain back on to the domain.

hermit2

Figure 3.3: The definition of an operator and its Hermitian conjugate

As can be gleamed from Fig. 3.3, we can also use a basis in both the domain and codomain to use the matrix representation of linear operators (3.1,3.2), and find that the matrix representation of an operator satisfies the same relations as that for a finite matrix,

{({L}^{†})}_{ ik} = {({L}_{ki})}^{∗}.

hermit3

Figure 3.4: A schematic representation of a self-adjoint operator.

A final important definition is that of

A self-adjoint or hermitian operator L equals its adjoint,
{L}^{†} = L.

Thus we also require that domain and codomain coincide, see Fig. 3.4.

[forward][up]