5.1 Basic integration

There are two ways of thinking about integration, and they both have their uses. The one we shall concentrate on here, is integration as the inverse of differentiation, also call indefinite integration,
∙ Indefinite integral

where F is the inverse derivative (also called “primitive”) of f.

Example 5.1: 

Integrate 4{x}^{3}.

Solution: 

4{x}^{3} = {d({x}^{4})\over dx} , so \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits 4{x}^{3}dx = {x}^{4} + c

This type of integration is called an indefinite integral. We always get a constant of integration (in this case “c”) for an indefinite integral.

Note: The result of \mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits f(x)dx is another function of x.
∙ Definite integral
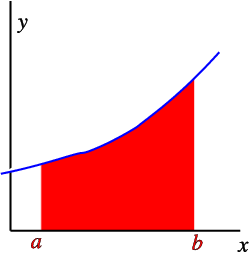
A definite integral is related to the area under a curve (see Fig. ??)

Figure 5.1: The area under a curve.

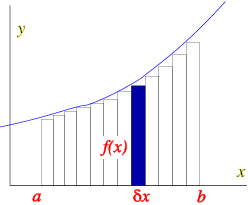
Plot the curve y = f(x), as in Fig. 5.1. The shaded area under curve between x = a and b equal a number A. We can calculate this as

(This is called a definite integral.) This is defined as the sum from x = a to x = b of the area of all the small strips under the curve, in the limit that they become vanishingly thin.

The two definitions are related by the
∙ Fundamental theorem of calculus

Example 5.2: 

Find area under curve y = 2{e}^{3x} between x = −1 and x = 1.

Solution: 

The area is given by the integral

\begin{eqnarray*} A& =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−1}^{1}2{e}^{3x}\kern 1.66702pt dx %& \\ & =& 2{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−1}^{1}{e}^{3x}dx %& \\ & =& 2{\left ({e}^{3x}∕3\right )}_{ −1}^{1} %& \\ & =& 2({e}^{3}∕3 − {e}^{−3}∕3)%& \\ & ≈& 13.3572\quad . %& \\ \end{eqnarray*}

Note: There is no constant of integration in a definite integral.

Note: The result is a number not a function.

Final Remark: Some integrals can never be done in terms of known functions.

Example 5.3: 

\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits {e}^{{x}^{2} }\kern 1.66702pt dx, {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{1}^{2}1∕(x +\mathop{ cos}\nolimits x)dx. For these a numerical method will give results for a definite integral, e.g., a computer version of summing the area of the strips under a curve.

5.1.1 standard integrals

We can use the “inverse derivative” to look up standard derivatives from right to left, to get a table of integrals. Many of the integrals in the formula book were obtained this way, Some examples:

Figure 5.2: A piston in a cylinder

Let us look at an interesting physics example of integration.

Example 5.4: 

A piston is moved in a cylinder containing an ideal gas (see Fig. 5.2). Calculate the work done as the enclosed volume changes.

Solution: 

The work done is force times distance. The maginitude of the force is pressure times ares, F = P × A. If we move the piston by a distance δx, the work done is thus PAδx = PδV . Thus

W ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{{V }_{0}}^{{V }_{1} }P(V )\kern 1.66702pt dV \quad .

For an ideal gas P(v) = A∕V , and we find that

W ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{{V }_{0}}^{{V }_{1} } {A\over V }\kern 1.66702pt dV = A{\left [\mathop{ln}\nolimits (V )\right ]}_{{V }_{0}}^{{V }_{1} } = A(\mathop{ln}\nolimits {V }_{1} −\mathop{ ln}\nolimits {V }_{0}) = A\mathop{ln}\nolimits ({V }_{1}∕{V }_{0})\quad .

Note that the argument of the logarithm is dimensionless. This is true of any mathematical functions we write.