[forward][up]

3.1 Functions of several variables

Definition: A real function f({x}_{1},...,{x}_{n}) of n real variables {x}_{1},...,{x}_{n} is a map

\begin{eqnarray} f : {R}^{n} → R,\quad x := ({x}_{ 1},{x}_{2},...,{x}_{n}) → f(x) = f({x}_{1},...,{x}_{n}).& & %&(3.1) \\ \end{eqnarray}

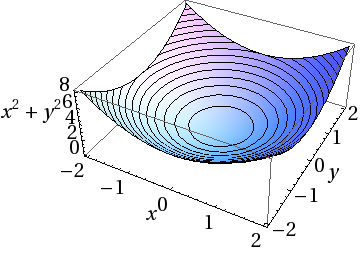
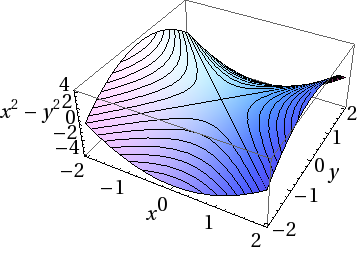
In the following, we mainly discuss functions of two variables {x}_{1} and {x}_{2}, i.e. the case n = 2. Such functions can be represented by a three–dimensional surface plot, where the value z = f(x,y) at each point (x,y) in the x–y plane is plotted in the z–direction over the x–y plane. Here are two examples:

paraboloid saddle

Figure 3.1: Examples of functions f(x,y) of two variables x and y: Paraboloid f(x,y) = {x}^{2} + {y}^{2} (LEFT), saddle f(x,y) = {x}^{2} − {y}^{2} (RIGHT).
The Paraboloid f(x,y) = {x}^{2} + {y}^{2}

paraboloid

Figure 3.2: Paraboloid f(x,y) = {x}^{2} + {y}^{2}.

We can understand this graph as follows:

1. If we keep y fixed and change x, we have a parabola for each y, e.g.

\begin{eqnarray*} f(x,0)& =& {x}^{2} %& \\ f(x,−1)& =& {x}^{2} + 1%& \\ f(x,1)& =& {x}^{2} + 1%& \\ f(x,2)& =& {x}^{2} + 4%& \\ ...& & %& \\ \end{eqnarray*}

If we keep x fixed and change y, we have a parabola for each x, e.g.

\begin{eqnarray*} f(0,y)& =& {y}^{2} %& \\ f(−1,y)& =& 1 + {y}^{2}%& \\ f(1,y)& =& 1 + {y}^{2}%& \\ f(3,y)& =& 9 + {y}^{2}%& \\ ...& & %& \\ \end{eqnarray*}

These are cross–sections of the graph in x and y direction. It is important that you learn to visualise these cross–sections in your mind.

2. If we keep the value of the function fixed, i.e. z = f(x,y) = {z}_{0} = const > 0, we find circles

\begin{eqnarray}{ z}_{0} = f(x,y) = {x}^{2} + {y}^{2}.& & %&(3.2) \\ \end{eqnarray}

Exercise: visualise these circles from the figure above. What are the radii of the circles for a given height f(x,y) = {z}_{0}?

The Saddle f(x,y) = {x}^{2} − {y}^{2}

saddle

Figure 3.3: Saddle f(x,y) = {x}^{2} − {y}^{2}.

We can understand this graph as follows:

1. If we keep y fixed and change x, we have a parabola for each y, e.g.

\begin{eqnarray*} f(x,0)& =& {x}^{2} %& \\ f(x,−1)& =& {x}^{2} − 1%& \\ f(x,1)& =& {x}^{2} − 1%& \\ f(x,2)& =& {x}^{2} − 4%& \\ ...& & %& \\ \end{eqnarray*}

These are parabolas bending upwards but with their origin shifted to negative values.

If we keep x fixed and change y, we have a parabola for each x, e.g.

\begin{eqnarray*} f(0,y)& =& −{y}^{2} %& \\ f(−1,y)& =& 1 − {y}^{2}%& \\ f(1,y)& =& 1 − {y}^{2}%& \\ f(3,y)& =& 9 − {y}^{2}%& \\ ...& & %& \\ \end{eqnarray*}

These are parabolas bending downwards but with their origin shifted to positive values. We can built up the whole graph from these cross-sections. The interesting thing is that we understand the global shape of the surface f(x,y), i.e. its saddle–shape, only form ‘glueing’ together all the cross–sections.

The most interesting points in both the paraboloid and the saddle are the extrema at (x,y) = (0,0): for the paraboloid, this is a global minimum, for the saddle this is neither a minimum (it is a minimum in x–direction only) nor a maximum (it is a maximum in y–direction only): it is a saddle–point.

3.1.1 Symmetries

The Paraboloid f(x,y) = {x}^{2} + {y}^{2}

We consider the circle of fixed radius r,

\begin{eqnarray}{ r}^{2} = {x}^{2} + {y}^{2}& & %&(3.3) \\ \end{eqnarray}

in the x–y plane. For all points on this circle, the function f(x,y) = {x}^{2} + {y}^{2} has the same value f(x,y) = {r}^{2}. A rotation of a point (x,y) on this circle around the origin (x,y) = (0,0) does not alter f(x,y). In fact, if we rotate f(x,y) continuously around the z–axis, f(x,y) remains invariant. The function f(x,y) has a continous rotation symmetry. Therefore, it is also called ‘rotational paraboloid’ sometimes. We can build up the whole surface f(x,y) from rings with radius r stacked on top of each other in the z–direction. Again, when dealing with functions of more than one variable, it is important that you develop this geometric kind of thinking.

The function f(x,y) also has other symmetries: f(x,y) = f(−x,y) = f(x,−y) = f(−x,−y) (reflection of one or two of its variables).

[forward][up]