Chapter 8
Symmetries and particle physics

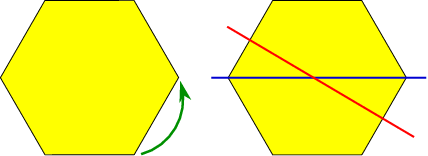
Symmetries in physics provide a great fascination to us – one of the hang-ups of mankind. We can recognise a symmetry easily, and they provide a great tool to classify shapes and patterns. There is an important area of mathematics called group theory, where one studies the transformations under which an object is symmetric. In order to make this statement seem less abstract, let me look at a simple example, a regular hexagon in a plane. As can be seen in figure Fig. 8.5 , this object is symmetric (i.e., we can’t distinguish the new from the old object) under rotations around centre over angles of a multiple of $60^{\circ }$, and under reflection in any of the six axes sketched in the second part of the figure.

This work is a UK OER project as part of the Skills for Scientists project. Please contact Niels Walet for more information

This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 2.0 Generic License