6.3 QED: photon couples to
We know that electrons and positrons have charge and thus we need to include electrodynamics in the relativistic quantum theory of the electron. That is even more clear when we take into account that an electron and positron can annihilate by emitting two photons (the well-known 511 keV lines),
| (6.15) |
Question: Why not one photon?
There is a natural way to describe this coupling, in a so-called Lagrangian approach, which I shall not discuss here. It teaches us that an electron can emit a photon, as indicated figure 6.3 .
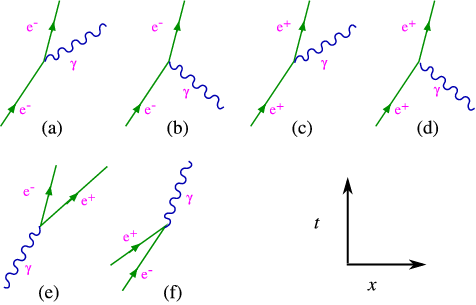
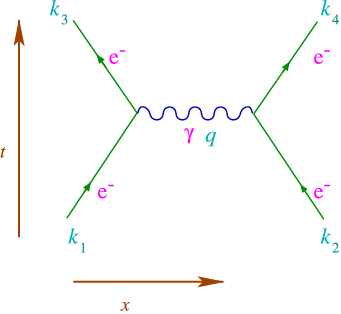
The diagrams in figure 6.3 are usually referred to as a Feynman diagrams, and the process depicted in (a) is usually called Bremsstrahlung, the one in (b) annihilation. With such a diagram comes a recipe for calculating it (called the Feynman rule). A key point is that energy and momentum are conserved in all reactions. Let us look at what happens when another nearby electron absorbs the photon, as in figure 6.4
Of course there are two possibilities: The left electron can emit the photon to the right one, or absorb one that is emitted by the right one. This is related to the time-ordering of interactions. One of the advantages of Feynman diagrams is that both these possibilities are described in one Feynman diagram. Thus the time in this diagram should only be interpreted in the sense of the external lines, what are the particles in and out. It is also very economical if we have more and more particles emitted and absorbed.
Since the emitted photon only lives for a short time, , its energy cannot be determined exactly due to the uncertainty relation
| (6.16) |
Thus even though the sum of the initial (four) momenta, equals the sum of the final ones, , we find that the photon does not have to satisfy
| (6.17) |
Such a photon is called virtual or “off mass-shell”, since it does not satisfy the mass-energy relations. This is what gives rise to the Coulomb force.