Chapter 4
Bound states of the square well
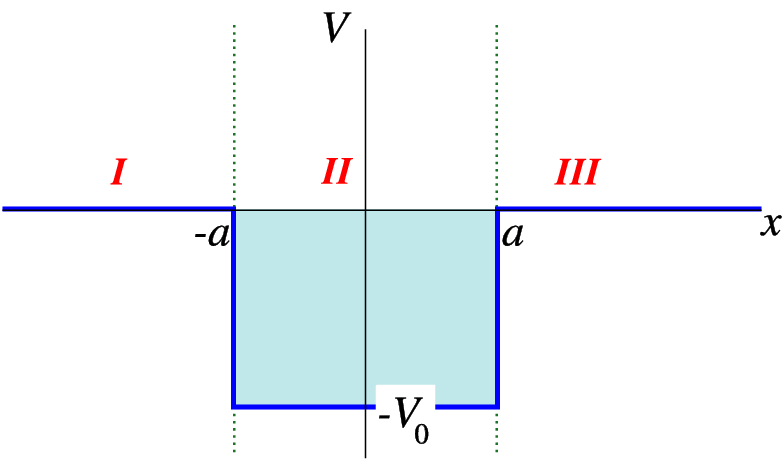
One of the simplest potentials to study the properties of is the so-called square well potential,
| (4.1) |
We define three areas, from left to right I, II and III. In areas I and III we have the Schrödinger equation
| (4.2) |
whereas in area II we have the equation
| (4.3) |
__________________________________________________________________
________________________________________________________________________________________________________Let us first look at . In that case the equation in regions and can be written as
| (4.8) |
where
| (4.9) |
The solution to this equation is a sum of sines and cosines of , which cannot be normalised: Write ( , , complex) and calculate the part of the norm originating in region ,
We also find that the energy cannot be less than , since we vannot construct a solution for that value of the energy. We thus restrict ourselves to . We write
| (4.11) |
The solutions in the areas I and III are of the form ( )
| (4.12) |
In region II we have the oscillatory solution
| (4.13) |
Now we have to impose the conditions on the wave functions we have discussed before, continuity of and its derivatives. Actually we also have to impose normalisability, which means that (exponentially growing functions can not be normalised). As we shall see we only have solutions at certain energies. Continuity implies that
Tactical approach: We wish to find a relation between and (why?), removing as manby of the constants and . The trick is to first find an equation that only contains and . To this end we take the ratio of the first and third and second and fourth equation:
We can combine these two equations to a single one by equating the right-hand sides. After deleting the common factor , and multiplying with the denominators we find
which simplifies to
| (4.17) |
We thus have two families of solutions, those characterised by and those that have .