[forward][back][up]

6.2 Potential step

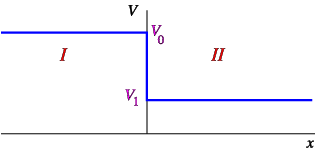
Consider a potential step

V (x) = \left \{\array{ {V }_{0}&x < 0 \cr {V }_{1}&x > 0 } \right .
(6.3)

step1


Figure 6.1: The step potential discussed in the text

Let me define

\begin{eqnarray}{ k}_{0}& =& \sqrt{{2m\over {ℏ}^{2}} (E − {V }_{0})},%&(6.4) \\ {k}_{1}& =& \sqrt{{2m\over {ℏ}^{2}} (E − {V }_{1})}.%&(6.5) \\ \end{eqnarray}

I assume a beam of particles comes in from the left,

ϕ(x) = {A}_{0}{e}^{i{k}_{0}x},\kern 2.77695pt \kern 2.77695pt x < 0.
(6.6)

At the potential step the particles either get reflected back to region I, or are transmitted to region II. There can thus only be a wave moving to the right in region II, but in region I we have both the incoming and a reflected wave,

\begin{eqnarray} {ϕ}_{I}(x)& =& {A}_{0}{e}^{i{k}_{0}x} + {B}_{ 0}{e}^{−i{k}_{0}x},%&(6.7) \\ {ϕ}_{II}(x)& =& {A}_{1}{e}^{i{k}_{1}x}. %&(6.8) \\ \end{eqnarray}

We define a transmission and reflection coefficient as the ratio of currents between reflected or transmitted wave and the incoming wave, where we have canceled a common factor

R = {|{B}_{0}{|}^{2}\over |{A}_{0}{|}^{2}} \kern 2.77695pt \kern 2.77695pt \kern 2.77695pt T = {{k}_{1}|{A}_{1}{|}^{2}\over { k}_{0}|{A}_{0}{|}^{2}}.
(6.9)

Even though we have given up normalisability, we still have the two continuity conditions. At x = 0 these imply, using continuity of ϕ and {d\over dx}ϕ,

\begin{eqnarray} {A}_{0} + {B}_{0}& =& {A}_{1}, %&(6.10) \\ i{k}_{0}({A}_{0} − {B}_{0})& =& i{k}_{1}{A}_{1}.%&(6.11) \\ \end{eqnarray}

We thus find

\begin{eqnarray} {A}_{1}& =& {2{k}_{0}\over { k}_{0} + {k}_{1}}{A}_{0},%&(6.12) \\ {B}_{0}& =& {{k}_{0} − {k}_{1}\over { k}_{0} + {k}_{1}}{A}_{0},%&(6.13) \\ \end{eqnarray}

and the reflection and transmission coefficients can thus be expressed as

\begin{eqnarray} R& =&{ \left ({{k}_{0} − {k}_{1}\over { k}_{0} + {k}_{1}}\right )}^{2},%&(6.14) \\ T& =& {4{k}_{1}{k}_{0}\over { ({k}_{0} + {k}_{1})}^{2}}.%&(6.15) \\ \end{eqnarray}

Notice that R + T = 1!

stepTR


Figure 6.2: The transmission and reflection coefficients for a square barrier.

In Fig. 6.2 we have plotted the behaviour of the transmission and reflection of a beam of Hydrogen atoms impinging on a barrier of height 2 meV.

[forward][back][up]