Figure 7.2: The correspondence between quantum and classical probabilities
One of the interesting questions raised by the fact that we can solve both the quantum and the classical problem exactly for the harmonic oscillator, is “Can we compare the Classical and Quantum Solutions?”
In order to do that we have to construct a probability for the classical solution. The variable over which we must average to get such a distribution must be time, the only one that remains in the solution. For simplicity look at a cosine solution, a sum of sine and cosines behaves exactly the same (check!). We thus have, classically,
|
x = A\mathop{cos}\nolimits (ωt),\qquad v = −Aω\mathop{sin}\nolimits (ωt).
| (7.29) |
If we substitute this in the energy expression, E = {1\over 2}m{v}^{2} + {1\over 2}m{ω}^{2}{x}^{2}, we find that the energy depends on the amplitude A and ω,
|
E(A) = {1\over
2}m{A}^{2}{ω}^{2}{\mathop{ sin}\nolimits }^{2}(ωt) + {1\over
2}m{ω}^{2}{A}^{2}{\mathop{ cos}\nolimits }^{2}(ωt) = {1\over
2}m{ω}^{2}{A}^{2}
| (7.30) |
Now the probability to find the particle at position x, where − A < x < A is proportional to the time spent in an area dx around x. The time spent in its turn is inversely proportional to the velocity v
|
{P}_{\mathrm{class}}(x)dx ∝ {1\over
|v(x)|}dx
| (7.31) |
Solving v in terms of x we find
|
|v(x)| = ω\sqrt{{A}^{2 } − {x}^{2}}
| (7.32) |
Doing the integration of 1∕v(x) over x from − A to A we find that the normalised probability is
|
{P}_{\mathrm{class}}(x)dx = {1\over
π\sqrt{{A}^{2 } − {x}^{2}}}dx.
| (7.33) |
We now would like to compare this to the quantum solution. In order to do that we should consider the probabilities at the same energy,
|
{1\over
2}m{ω}^{2}{A}^{2} = ℏω(n + {1\over
2}),
| (7.34) |
which tells us what A to use for each n,
|
A(n) = \sqrt{ {ℏ\over
mω}(2n + 1)}.
| (7.35) |
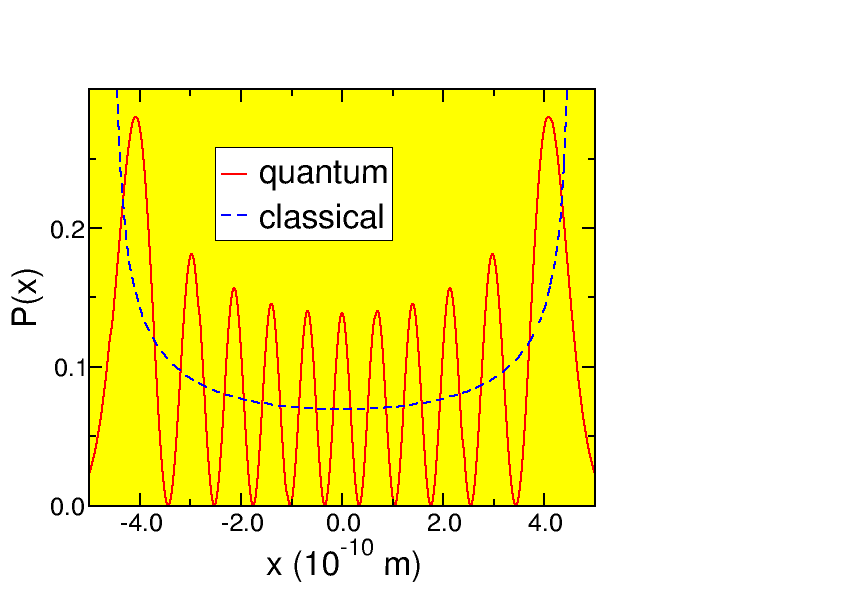
So let us look at an example for n = 10. Suppose we choose m and ω such that \sqrt{ {ℏ\over mω}} = 1{0}^{−10}\ \mathrm{m}. We then get the results shown in Fig. 7.2, where we see the correspondence between the two functions.