Figure 11.2: The probability to find a certain value of
r
for the first two Harmonic oscillator wave functions.
Clearly the probability density to find an electron at point x is
|
P(x) = R{(r)}^{∗}R(r),
| (11.22) |
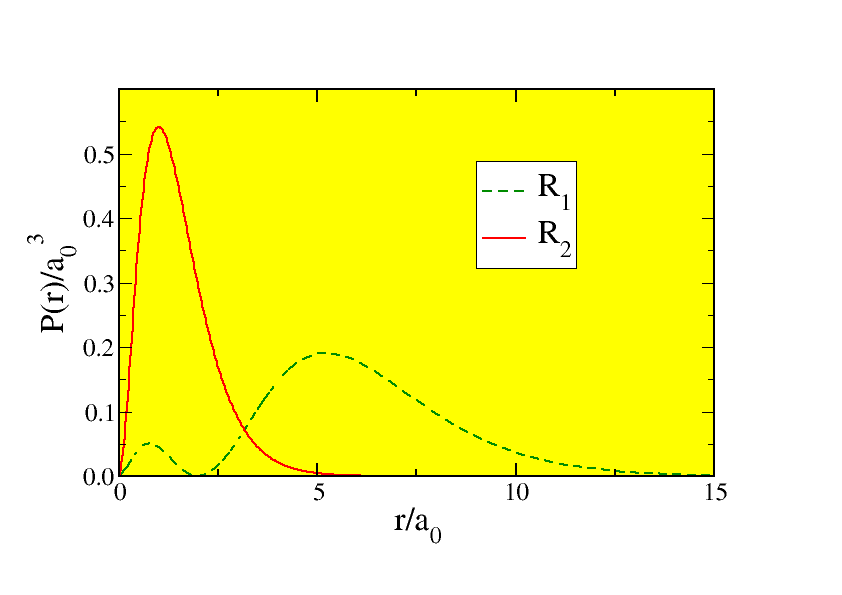
but what is the probability to find the electron at a distance r from the proton? The key point to realise is that for each value of r the electron can be anywhere on the surface of a sphere of radius r, so that for larger r more points contribute than for smaller r. This is exactly the source of the factor 4π{r}^{2} in the normalisation integral. The probability to find a certain value of r is thus
|
P(r) = 4π{r}^{2}R{(r)}^{∗}R(r).
| (11.23) |
These probabilities are sketched in Fig. 11.2. The peaks are of some interest, since they show where the electrons are most likely to be found. Let’s investigate this mathematically:
|
{P}_{1} = 4{r}^{2}∕{a}_{
0}^{3}{e}^{−2r∕{a}_{0}
}.
| (11.24) |
if we differentiate with respect to r, we get
|
{d\over
dr}{P}_{1} = {4\over {
a}_{0}^{3}}(2r{e}^{−2r∕{a}_{0}
} − 2{r}^{2}∕{a}_{
0}{e}^{−2r∕{a}_{0}
}).
| (11.25) |
This is zero at r = {a}_{0}. For the first excited state this gets a little more complicated, and we will have to work harder to find the answer.