Advanced Quantum Mechanics II PHYS 40202

$\newcommand{\lyxlock}{} \newcommand{\rvec}[1]{\underset{\unicode{x3030}}{#1}} \renewcommand{\vec}[1]{\boldsymbol{#1}} \newcommand{\lvec}[1]{\overrightarrow{#1}} \newcommand{\unitvec}[1]{\hat{\boldsymbol{#1}}} \newcommand{\mat}[1]{\mathbf{#1}} \newcommand{\ket}[1]{\left|#1\right\rangle } \renewcommand{\bra}[1]{\left\langle #1|\right|} \renewcommand{\braket}[2]{\left\langle #1|#2\right\rangle} \renewcommand{\braOket}[3]{\left\langle #1|#2|#3\right\rangle } \renewcommand{\ketbra}[2]{\left|#1\rangle\langle#2\right|} \renewcommand{\Clebsch}[6]{\left\langle#1,#2|#3,#4;#5,#6\right\rangle} \renewcommand{\propagator}[2]{K(#1;#2)} \newcommand{\frontmatter}{} \newcommand{\mainmatter}{} \newcommand{\textbook}{} \newcommand{\backmatter}{} \newcommand{\clearpage}{} \newcommand{\addcontentsline}{}$

Warning: MathJax requires JavaScript to correctly process the mathematics on this page. Please enable JavaScript on your browser.

To be used in future

Prev Section 4.3: Gauge transformations and Gauge invariance Up Chapter 4: Charged Particles and Electromagnetic Fields Section 4.5: Coupling of light to atoms and nuclei: multipole couplings Next

4.4 Landau Levels

We now consider a charged particle in a homogeneous magnetic field↓ in the

direction,

. One (of many) possible forms of the vector potential corresponding to this field can be given using the “↓↓Landau gauge”

and the Hamiltonian in coordinate representation can be written as

where we the final term originates in the fact hat

and

do not commute!

When solving for the eigenstates of this Hamiltonian, we can first of all remove the

-component of the problem, which completely decouples from the

motion, and we can describe the motion by a plane wave,

We can now concentrate on the in-plane motion, and just discuss the movement of the particle in the

plane; since we find

, we can also diagonalise

but we pay a price, since the

wave equation now depends on

, [P] [P]

is the energy for

motion only.

Here

is the cyclotron frequency [Q] [Q] The harmonic oscillator length parameter associated with this is

Since the Hamiltonian above is that of a shifted harmonic oscillator, we find

where

is the

th eigenstate of the harmonic oscillator with frequency

; and thus

with energy

Thus all states with the same

, i.e., where we fix the

wave function but leave the

wave function as yet undetermined, are degenerate. The set of degenerate states for a fixed value of

is called a ↓Landau level.

4.4.1 (Integer) Quantum Hall Effect↓

Let us first consider the classical physics of conductance in a 2D conductor (in the jargon of the field a “2D electron gas↓↓” or 2DEG) in a perpendicular magnetic field. If we impose a current on a sample with conductivity

, we can show that it satisfies the equation,

using the fact that current is driven by the Lorentz force

. The material property

can be linked to the mean-time

between scattering of an individual electron of the conductor, and the charge density

We now bring all the current terms to one side of the equation,

and we find that the resistance tensor takes the form

where the off-diagonal terms show that in a magnetic field perpendicular to the sample, for a voltage in the

direction we will be able to measure a current in the

direction, proportional to the strength of the magnetic field! This is the “Hall current↓” of the classical Hall effect, and this is clearly a useful and practical way to measure magnetic fields.

Things are somewhat different if we look at the quantum version of this effect, which is done for samples at very low temperatures. The physical set up is straightforward: we have small area of relatively pure GaAs ↓embedded in Ga↓, where the GaAs behaves like a gas of 2D electrons. In a perpendicular magnetic field we should be able to distinguish the separate Landau levels, which now form bands of states. Residual forces lead to a broadening of the Hall states, but the principle idea remains correct. We first must figure out how many particles each Landau level holds (or number of particles per unit area). Mathematically, we need to look at periodic boundary conditions, and count the states allowed per level. To do this analytically is quite hard [R] [R] See Yoshioka, Halperin, Lee, Phys. Rev. Lett. 50 (1983) 1219, and Haldane and Rezayi, Phys. Rev. B 31 (1985) 2529, but the answer can fortunately be found by a simple argument:

The density of states in 2D (without magnetic field, at very low temperatures) is given by

where

is the Fermi energy. If we have a large number of Landau levels below the Fermi energy, we find that we can approximate the number

of Landau states below the Fermi level as (ignoring the subtraction of

, which is assumed to be much smaller than

)

We believe that the number of states below the Fermi level is independent of the magnetic field

—since

is fixed externally, the number of states must remain constant. We thus must require that each Landau level contains (we use the symbol

for area)

states, so that (↓) and (↓) give the expression (↓).

This suggests that the area of each Landau level scales like

; since classically electrons move in circles, whose radius shrinks in this way, that would be a natural prediction of a Bohr-like model.

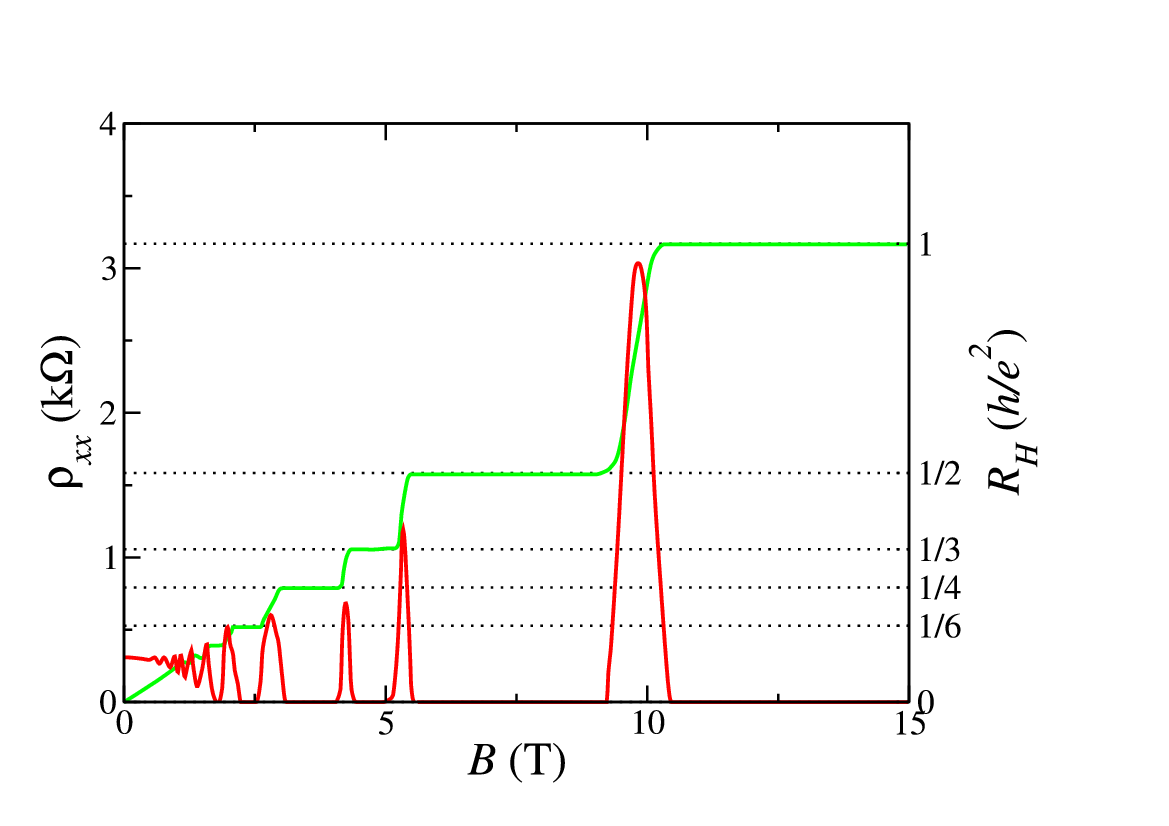
If the Landau levels are separated by an energy much larger than the intrinsic width of each state [S] [S] Of course, I haven’t explained why they get a width: interactions between electrons, temperature, ...., we will find that if the Fermi energy, which is imposed externally by the semiconductor the 2D electron gas is embedded in, lies either in between Landau levels or inside a Landau level, we get a very different behaviour, see Fig. 4.1↓.

Figure 4.1 Typical magnetic field dependence of

(red) and

(green)

One of the very important aspects of the integer quantum Hall effect is that it is actually best seen in a low purity material (usually GaAs), where most of the Landau levels are “pinned” to defects or impurities, and very few electronic states extend across the whole system. In the limit of a very impure system, just one state at the middle of the band is such an “extended state”. The width of the band itself is caused by the residual Coulomb interaction between electrons and of the electrons with the lattice.

If we follow the discussion of conductance in (↓) above, we see that the conductance diverges when the mean time between scatterings goes to infinity. Since at low temperatures transport only takes place near the Fermi level, this happens exactly when the Fermi level lies in a gap, since any electrons at this energy have no nearby states to scatter with. This explains the peaks and valleys in the diagonal conductance. The peaks grow since the number of states in a Landau level grows proportionally to

. Of more practical relevance is the Hall conductance; this is quantised for the simple reason that all electrons in the (

) occupied Landau levels contribute, which give a jump each time a Landau level moves through the Fermi energy. We find that the Hall resistance is

where

is the number of Landau levels below the Fermi energy.

This equation contains the von Klitzing constant↓

which is used to fix the measurement of resistance, since it can be measured very precisely from the plateaus in the quantum Hall effect.

In order to show you the basic aspects of the integer quantum Hall effect, look at the Mathematica-based simulation on the course site.

Prev Section 4.3: Gauge transformations and Gauge invariance Up Chapter 4: Charged Particles and Electromagnetic Fields Section 4.5: Coupling of light to atoms and nuclei: multipole couplings Next