3.8 Work

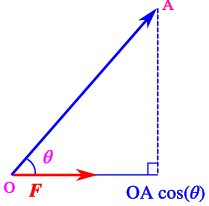
In mechanics the work performed by a force is defined as the product of the magnitude of the force times the distance moved in the direction of the force.

Figure 3.14: The work done by the force F if a mass moves from O to A equals OA ⋅ F ⋅\mathop{ cos}\nolimits θ.

From Fig. 3.14 we see that, since the component of OA along the line of force is OA\mathop{cos}\nolimits θ, where OA is the distance d travelled, the work is W = d\kern 1.66702pt \mathop{cos}\nolimits θ\kern 1.66702pt F = d⋅F, and thus work can be evaluated as an innerproduct.

Example 3.9: 

A force F = 2i + 3j −k\text{ N} is applied to a particle which is moving along a wire OAB where OA and AB are straight, and the points A and B are A = (1,0,0)\text{ m} and B = (2,2,−2)\text{ m}. Find the work done.

Solution: 

Along the line OA the work done is F ⋅\overrightarrow{ OA},

{W}_{1} = (2,3,−1) ⋅ (1,0,0) = 2\text{ J}.

Along the line AB, \overrightarrow{AB} = (1,2,−1), and the work done is

{W}_{2} = (2,3,−1) ⋅ (1,2,−1) = 2 + 6 + 1 = 9\text{ J}.

The total work is thus

\class{boxed}{W = 2 + 9 = 11\text{ J}. }