3.9 The vector product

We have now looked extensively at the scalar product, and now look at the vector product, that returns a vector. Two standard notations are used

We shall use the first notation. Other terms used are “cross product” or “outer product”.

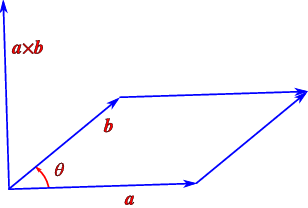
The vector product of two vectors a and b is defined as a vector, see Fig. 3.15,

• of magnitude ab|\mathop{sin}\nolimits θ|
• of a direction orthogonal to both a and b, so that a, b and a×b form a right-handed set

Figure 3.15: The definition of the outer product.

The magnitude of the outer product is exactly equal to the area of the parallelogram with sides a and b, A = ab\mathop{sin}\nolimits θ. calculation of the outer product in component form (to be discussed below) is thus an easy way to obtain this area.

Let n be a unit vector in the direction of a×b, then a×b = ab\mathop{sin}\nolimits θn. From the right handed rule we see that b×a = ab\mathop{sin}\nolimits θ(−n) = −a×b, i.e., the vector product is not commutative. Properties of the outer product:

1. For parallel vectors θ = 0 and so a×b = 0, in particular a×a = 0.
2. For orthogonal vectord, i.e., the angle θ between a and b is π∕2, any two of the vectors a, b and a×b are orthogonal.
3. The coordinate vectors i, j, k:
   i×i = j ×j = k ×k = 0.
   \eqalignno{ i×j & = k\qquad &j ×i & = −k. & & & & \cr j ×k & = i\qquad &k ×j & = −i. & & & & \cr k ×i & = j\qquad &i×k & = −j. & & & & }
4. From a×b = ab\mathop{sin}\nolimits θn we see that (na) ×b = (ma)b\mathop{sin}\nolimits θn = m(a×b).
5. a× (b + c) = a×b + a×c. Follows most easily from component form (see below).
6. Component form:
   Using a = {a}_{x}i + {a}_{y}j + {a}_{z}k and similar for vecb, we find
   \eqalignno{ c = &a×b & & \cr = &({a}_{x}i + {a}_{y}j + {a}_{z}k) × ({b}_{x}i + {b}_{y}j + {b}_{z}k) & & \cr = &{a}_{x}{b}_{x}i×i + {a}_{x}{b}_{y}i×j + {a}_{x}{b}_{z}i×k+ & & \cr &{a}_{y}{b}_{x}j ×i + {a}_{y}{b}_{y}j ×j + {a}_{y}{b}_{z}j ×k+ & & \cr &{a}_{z}{b}_{x}k ×i + {a}_{z}{b}_{y}k ×j + {a}_{z}{b}_{z}k ×k & & \cr = &i({a}_{y}{b}_{z} − {a}_{z}{b}_{y}) + j({a}_{z}{b}_{x} − {a}_{x}{b}_{z}) + k({a}_{x}{b}_{y} − {a}_{y}{b}_{x}) & & }

   This last line is often summarized in the form of a determinant

   \left |\array{ i & j &k\cr {a}_{ x}&{a}_{y}&{a}_{z} \cr {b}_{x}&{b}_{y}&{b}_{z} } \right | =\mathop{ det}\left (\array{ i & j &k\cr {a}_{ x}&{a}_{y}&{a}_{z} \cr {b}_{x}&{b}_{y}&{b}_{z} } \right ).

Example 3.10: 

Give a = (6,1,3) and b = (−2,0,4), find a×b.

Solution: 

a×b = i(1 ⋅ 4 − 3 ⋅ 0) + j(3 ⋅ (−2) − 6 ⋅ 4) + k(6 ⋅ 0 − (−1) ⋅ (−2)) = (4,−30,2).

Example 3.11: 

Find a×b given a = i + 2j −k, and b = 2i−j + k ,and find \hat{n} the unit vector perpendicular to a and b.

a×b =\mathop{ det}\left (\array{ i& 1 & 2\cr j& 2 &−1 \cr k&−1& 1} \right ).

Expand by Row 1: and we get i(2 − 1) −j(1 + 2) + k(−1 − 4) = i− 3j − 5k.

\begin{eqnarray*} \hat{n} = {a×b\over |a||b|}& =& {i− 3j − 5k\over \sqrt{ 1 + 9 + 25}} %& \\ & =& {1\over \sqrt{35}}(i− 3j − 5k)%& \\ \end{eqnarray*}

Other examples: