Figure 3.16: The parallelopipid related to the scalar triple product.
The inneer product a⋅b is a scalar, and we can’t use the result in further vector or dot products. The outer product a×b is a vector so it may be combined with a third vector c to form either a scalar product (a×b) ⋅c, or a vector product: (a×b) ×c.
We shall look at the scalar triple product,
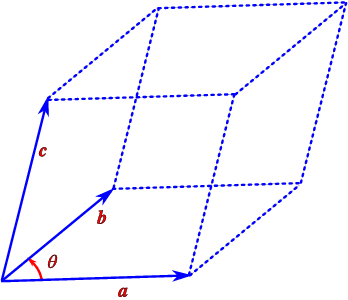
It is clearly a scalar quantity since \hat{n}⋅c is a number. It is particularly relevant to study the geometric interpretation, as in Fig. 3.16.
The quantity n⋅c is the height of the parallelopiped in that figure, adn we find that
where V is the volume of the parallelopiped. V is independent of the way it is calculated, i.e., any face may be used as base. Hence
Since scalar product is commutative
All the six expressions are equal! The ⋅ and the × may be interchanged as long as product is defined.
We know that
|
a×b = ({a}_{2}{b}_{3} − {a}_{3}{b}_{2})i + ({a}_{3}{b}_{1} − {a}_{1}{b}_{3})j + ({a}_{1}{b}_{2} − {a}_{2}{b}_{1})k,
|
then (a×b) ⋅c with c = {c}_{1}i + {c}_{2}j + {c}_{3}k,
|
(a×b)c = ({a}_{2}{b}_{3} − {a}_{3}{b}_{2}){c}_{1} + ({a}_{3}{b}_{1} − {a}_{1}{b}_{3}){c}_{2} + ({a}_{1}{b}_{2} − {a}_{2}{b}_{1}){c}_{3}
|
This can be put in determinant form,
|
\mathop{det}\left (\array{
{a}_{1}&{b}_{1}&{c}_{1}
\cr
{a}_{2}&{b}_{2}&{c}_{2}
\cr
{a}_{3}&{b}_{3}&{c}_{3} } \right )
|
Note that the order of the columns rows is the same as the order of the vectors. a, b and c in the STP.
Example 3.12:
Find (a×b) ⋅c
given a = i− 2j,
b = 3j + k,
c = i + j −k.
|
\mathop{det}\left (\array{
1 &0& 1\cr
−2 &3 & 1
\cr
0 &1&−1} \right ) =\mathop{ det}\left (\array{
3& 1\cr
1&−1
} \right )+\mathop{det}\left (\array{
−2&3\cr
0 &1} \right ) = −4−2 = −6
|
Important physical quantities represented by a vector product are
|
\class{boxed}{L = r ×p = mr ×v. }
|
|
\class{boxed}{F = qv ×B. }
|
|
\class{boxed}{T = r ×F. }
|