4.1 Assumed knowledge

4.1.1 First principles definition

Figure 4.1: The definition of the differential.

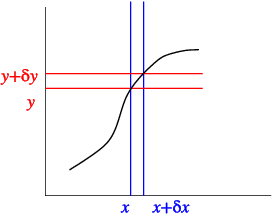
If y = f(x) and x increases from x to x + δx then the change in y is give by δy = f(x + δ) − f(x), see Fig. 4.1. The differential is defined as

4.1.2 Meaning as slope of a curve

Figure 4.2: The definition of the differential.

The derivative can also be interpreted as the slope of a curve, see Fig. 4.2. If the slope at a given point has an angle θ, we find that \mathop{tan}\nolimits θ is {dy\over dx}. In other words, the line y − {y}_{0} =\mathop{ tan}\nolimits θ\kern 1.66702pt (x − {x}_{0}) is tangent to the curve at ({x}_{0},{y}_{0}).

4.1.3 Differential of a sum

The differential of a sum is the sum of differentials,

4.1.4 Differential of product

There exists a simple rule to calculate the differential of a product,

E.g., if y = {x}^{2}\mathop{ sin}\nolimits x,

4.1.5 Differential of quotient

In the same way we can find a relation for the differential of a quotient,

E.g., if y = {\mathop{sin}\nolimits x\over x} ,

4.1.6 Function of a function (chain rule)

Often we take a function of a function. In such a case, where y = f(g(x)) we put z = g(x), and find

This rule is sometimes expressed in words as “the derivative of the function, times the derivative of its argument”, and you may know it as

Example 4.1: 

Find {dy\over dx} for y =\mathop{ cos}\nolimits (\mathop{ln}\nolimits x).

Solution: 

Put z =\mathop{ ln}\nolimits x so y =\mathop{ cos}\nolimits z,

{dy\over dx} = {dy\over dz},\quad {dz\over dx} = −\mathop{sin}\nolimits z {1\over x} = −{\mathop{sin}\nolimits (\mathop{ln}\nolimits x)\over x} \quad .

Example 4.2: 

Find {dy\over dx} for y ={\mathop{ sin}\nolimits }^{3}(2x − 1).

Solution: 

Put z =\mathop{ sin}\nolimits (2x − 1) so y = {z}^{3},

{dy\over dx} = {dy\over dz} {dz\over dx} = 3{z}^{2}2\mathop{cos}\nolimits (2x − 1) = 6{\mathop{sin}\nolimits }^{2}(2x − 1)\mathop{cos}\nolimits (2x − 1)\quad .

4.1.7 some simple physical examples

Example 4.3: 

Given that x(t) = 5{t}^{2}\text{ m}, find the velocity v(t) and the acceleration a(t).

Solution: 

Using the definitions of velocity as rate of change of position, we find that v =\dot{ x} = {dx\over dt} = 10t\text{ m/s}, and with acceleration as rate of change of velocity, we have a =\dot{ v} =\ddot{ x} = {dv\over dt} = 10\text{ m/s${}^{2}$}.

Example 4.4: 

For simple harmonic motion (SHM) x =\mathop{ cos}\nolimits (ωt). Find the velocity and acceleration.

Solution: 

Use the change rule for differentiation, v =\dot{ x} = −ω\mathop{sin}\nolimits (ωt), a =\dot{ v} = −{ω}^{2}\mathop{ cos}\nolimits (ωt)

4.1.8 Differential of inverse function

When we wish to calculate the differential of an inverse function, i.e, a function g such that g(f(x)) = x, we can use our knowledge of the derivative of f to find that of g.

Example 4.5: 

Find the derivative of y ={\mathop{ sin}\nolimits }^{−1}x.

Solution: 

We use y =\mathop{ sin}\nolimits (x) and calculate {dx\over dy} first,

{dx\over dy} = {\mathop{sin}\nolimits y\over dy} =\mathop{ cos}\nolimits y.

Now \mathop{cos}\nolimits y = ±\sqrt{1 −{\mathop{ sin} \nolimits }^{2 } y}, but the slope of the inverse sine is always positive. Thus

{dy\over dx} ={ \left ({dx\over dy}\right )}^{−1} = {1\over \sqrt{1 − {x}^{2}}}.

4.1.9 Maxima and minima

Figure 4.3: The meaning of a minimum and maximum.

At a maximum or minimum the slope is 0 so that {dy\over dx} = 0. To find which case it is, we look at {{d}^{2}y\over d{x}^{2}} , which can easily be done from a plot of the slope.

Example 4.6: 

Find all maxima and minima of y = x(3 − x) and determine their character.

Solution: 

We find that {dy\over dx} = x(−1) + (3 − x)1 = 3 − 2x. For a maximum or minimum the slope must be 0. This happens for 3 − 2x = 0, i.e., x = {3\over 2}. For that value of x, {{d}^{2}y\over d{x}^{2}} = −2. So the point x = 3∕2, y = 9∕4 is a (and the only) maximum.

4.1.10 Higher Derivatives

Higher derivatives are obtained by differentiation 2 or more times, {{d}^{2}y\over d{x}^{2}} = {d(dy∕dx)\over dx} , {{d}^{3}y\over d{x}^{3}} = {d({d}^{2}y∕d{x}^{2})\over dx} .

Example 4.7: 

y =\mathop{ ln}\nolimits x, {dy\over dx} = 1∕x, {{d}^{2}y\over d{x}^{2}} = −{1\over { x}^{2}} , {{d}^{3}y\over d{x}^{3}} = {2\over { x}^{3}} , etc.

Example 4.8: 

The equation for simple harmonic motion (SHM) is {{d}^{2}x\over d{t}^{2}} = −{ω}^{2}x. Prove that x = (A\mathop{cos}\nolimits ωt) + B\mathop{sin}\nolimits ωt satisfies this equation.

Solution: 

We must differentiate twice, start with first derivative, {dx\over dt} = (−ω)A\mathop{sin}\nolimits ωt + ωB\mathop{cos}\nolimits ωt, and find that

\begin{eqnarray*} {{d}^{2}x\over ∕} d{t}^{2}& =& −{ω}^{2}A\mathop{cos}\nolimits ω − {ω}^{2}B\mathop{sin}\nolimits ωt%& \\ & =& −{ω}^{2}(A\mathop{cos}\nolimits ωt + B\mathop{sin}\nolimits ωt)%& \\ & =& −{ω}^{2}x. %& \\ \end{eqnarray*}

QED.

N.B.: SHM not studied here, but in next semester. The constants A, B can only be obtained with extra input.