4.3 Vector functions

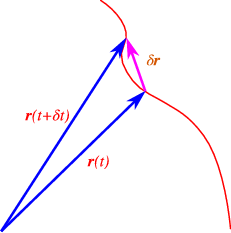
In physical (especially mechanics) problems we often have solutions in a form r = r(t), a “vector function”.

Example 4.12: 

A particle moves along a circle with uniform angular frequency, r = i\mathop{cos}\nolimits (ωt) + j\mathop{sin}\nolimits (ωt). Find the velocity.

Solution: 

If we are perfectly naive, we write v =\dot{ r} = −iω\mathop{sin}\nolimits (ωt) + jω\mathop{cos}\nolimits (ωt). This is actually correct!

The velocity is defined as the vector with as components the time-derivative of the components of the position vector,

Figure 4.4: A schematic representation of the derivative of a vector function.

It is actually quite illustrative to look at a graphical representation of the procedure, see Fig. ??. We notice there that the (vector) derivative of a vector function points is a vector that is tangent to (describes the local direction of) the curve: not a surprise since that is what velocity is!

Example 4.13: 

When a particle moves in a circle, find two independent way to show that r ⋅\dot{r} = 0.

Solution: 

1) Use the uniform motion example from above, and we find r ⋅v = −ω\mathop{cos}\nolimits (ωt)\mathop{sin}\nolimits (ωt) + ω\mathop{sin}\nolimits (ωt)\mathop{cos}\nolimits (ωt) = 0. This is not a general answer though!
2) Write r ⋅r = \text{constant}. (Definition of circle!) Then, by differentiating both sides of the relation (in the “other” order), we find

\eqalignno{ 0 & = {dr ⋅r\over dt} & & \cr & = {d{x}^{2} + {y}^{2} + {z}^{2}\over dt} & & \cr & = 2x{dx\over dt} + 2y{dy\over dt} + 2z{dz\over dt} & & \cr & = 2r ⋅\dot{r}. & & }

and we have the desired results.

Example 4.14: 

Find the velocity of a particle that moves from {r}_{1} = (1,2,3) to {r}_{2} = (3,6,7) in 2\text{ s} along a straight line with constant velocity. Also find the position 5\text{ s} after passing {r}_{1},

Solution: 

Clearly r ={ r}_{1} + vt if the particle is at point 1 at t = 0, We get, substituting t = 2;

(3,6,7) = (1,2,3) + v2,

from which we conclude (solving for each component separately) that v = (1,2,2). At time t = 5 we have

r = (1,2,3) + (1,2,2)5 = (6,12,13).

4.3.1 Polar curves

Things get slightly more involved (but quite relevant!) when we look at curves in polar coordinates, i.e., specified by r(t) and θ(t). From r = r\mathop{cos}\nolimits (θ)i + r\mathop{sin}\nolimits (θ)j we find that

The first unit vector is indeed the one parallel to r; the second one is defined from its expression. There is some interesting mathematics going on over here,

This is often used to say that r and θ are orthogonal coordinates, at each point they are associated with different, but always orthogonal directions!

Example 4.15: 

Express the velocity of a particle moving in an elliptic (Kepler) orbit,

r = {1\over 1 −{1\over 2}\mathop{ cos}\nolimits (θ)},

in turn of \dot{θ}. Now calculate the kinetic energy of the particle.

Solution: 

Obviously r = {\mathop{cos}\nolimits θ\over 1−{1\over 2}\mathop{ cos}\nolimits (θ)}i + {\mathop{sin}\nolimits θ\over 1−{1\over 2}\mathop{ cos}\nolimits (θ)}j. Now differentiate w.r.t. t using the chain and quotient rules:

\eqalignno{ r & =\dot{ θ}\left ({−\mathop{sin}\nolimits θ(1 −{1\over 2}\mathop{ cos}\nolimits (θ)) −\mathop{ cos}\nolimits θ{1\over 2}\mathop{ sin}\nolimits θ\over {(1 −{1\over 2}\mathop{ cos}\nolimits (θ))}^{2}} i + {\mathop{cos}\nolimits θ(1 −{1\over 2}\mathop{ cos}\nolimits (θ)) −\mathop{ sin}\nolimits θ{1\over 2}\mathop{ sin}\nolimits θ\over {(1 −{1\over 2}\mathop{ cos}\nolimits (θ))}^{2}} j\right ) & & \cr & = {\dot{θ}\over { (1 −{1\over 2}\mathop{ cos}\nolimits (θ))}^{2}}\left ((−\mathop{sin}\nolimits θ)i + (\mathop{cos}\nolimits (θ) −{1\over 2})j\right ). & & }

The kinetic energy is thus found to be

\eqalignno{ K = {1\over 2}m{v}^{2} & = {1\over 2}m {{(\dot{θ})}^{2}\over { (1 −{1\over 2}\mathop{ cos}\nolimits (θ))}^{4}}({\mathop{sin}\nolimits }^{2}θ +{\mathop{ cos}\nolimits }^{2}θ −\mathop{ cos}\nolimits θ + {1\over 4}) & & \cr & = {1\over 2}m{(\dot{θ})}^{2} {{5\over 4} −\mathop{ cos}\nolimits θ\over { (1 −{1\over 2}\mathop{ cos}\nolimits (θ))}^{4}}. & & }