2.1 Powers, logs, exponentials

2.1.1 Powers

Here we summarise the properties of the powers.

2.1.2 The product of two powers

First of all the product of two powers,

e.g., {3}^{2}{3}^{6} = {3}^{8}, and {3}^{1∕2}{3}^{3∕2} = {3}^{2} (we see that x and y do not have to be integers (whole numbers)). Question: Evaluate {5}^{7∕10}{5}^{3∕10}.

The power of a power

If we take the power of a power, we multiply the exponents,

e.g., {({2}^{3})}^{2} = {8}^{2} = 64 = {2}^{3×2} = {2}^{6} = 64. This again works for x,y not integers. Question: Evaluate {2}^{1∕4}{4}^{3∕8}.

Relation with roots

If the exponent is 1∕n we are taking the nth root of a,

e.g., {2}^{{1\over 2} } = \sqrt{2}, {2}^{{1\over 3} } = \root{3}\of{2}. If x = {a}^{{1\over n} } then {x}^{n} = a. This can be shown by taking both sides to the power n,

The number n is often taken to be an integer, but it does not have to be. (E.g., {({3}^{1∕9.5})}^{9.5} = 3.)

Zeroth power of a number

If we take a number to the power zero, we find

This follows from {a}^{0}{a}^{x} = {a}^{x+0} = {a}^{x}, and therefore {a}^{0} = 1. (Note that there is a slight problem with {0}^{0}: {0}^{x} = 0 for x > 0. One usually defines {0}^{0} = 1.)

Negative powers and fractions

If we take a number to a negative power, we write the result as a fraction involving a positive power,

since {a}^{−x}{a}^{x} = {a}^{−x+x} = {a}^{0} = 1. Therefore {a}^{−x} = {1\over { a}^{x}}. E.g., {2}^{−1} = 1∕2.

Common error

Remember that

and not

As an example, {2}^{3+5} = {2}^{8} = 64, but {2}^{3} + {2}^{5} = 8 + 32 = 40.

2.1.3 Exponential Function

The exponential function is a special case of a power, where y = {e}^{x}, with e = 2.71828.... (Euler’s number). One also writes \mathop{exp}\nolimits (x) instead of {e}^{x}.

Figure 2.1: A plot of the exponential \mathop{exp}\nolimits (x) and \mathop{exp}\nolimits (−x).

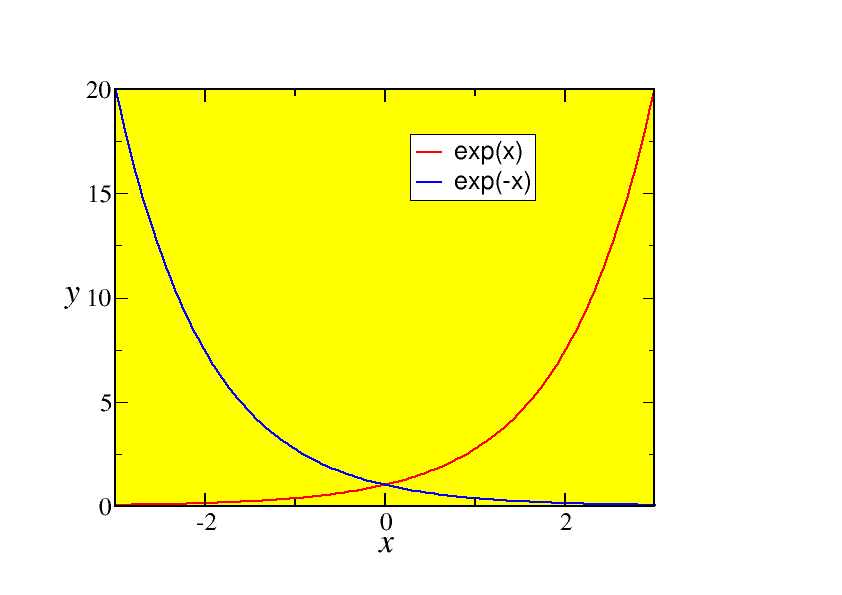
As we can see from Fig. 2.1, {e}^{x} is never less than 0 for any x. From the properties of powers we know that {e}^{−x} = {1\over { e}^{x}}. This function is also shown in Fig. 2.1, and is positive as well.

Differential (derivative w.r.t. x) of {e}^{x} is {e}^{x}, i.e.,

(This is the only function with the property that the derivative equals the function itself.)

If y = {e}^{ax} then {dy\over dx} = a{e}^{ax} (this is a form of the chain rule, which will be discussed later), e.g., if y = 3{e}^{7x} then {dy\over dx} = 3 × 7{e}^{7x} = 21{e}^{7x}.

Example 2.1: 

Discuss exponential growth/decay.

Solution: 

Exponential growth or decay is ruled by the form N(t) = {N}_{0}{e}^{at}. For a < 0 we have decay, for a > 0 we have growth. From the derivative, {dN\over dt} (t) = {N}_{0}a{e}^{at} = aN(t) we see that this arrises when the change in N is proportional to the number present. Examples are population growth, radioactive deay, ….

2.1.4 The Logarithmic Function

Relation between Logs and Exponentials

Figure 2.2: A plot of the natural logarithm \mathop{ln}\nolimits (x) and its derivative 1∕x.

A graph of the logarithm is shown in Fig. 2.2. If we swap the x and y axes, we recognise the exponential. Normally we use logs to base e (inverse of {e}^{x})- called natural logarithms, hence the name \mathop{ln}\nolimits (x), but we also write

Logs to other bases

Just as y =\mathop{ ln}\nolimits x ⇒ x = {e}^{y} for the logarithm corresponding to base e (i.e., the inverse of {e}^{x}) for other bases we have y ={ \mathop{log}\nolimits }_{a}x ⇒ x = {a}^{y}. Here we use the notation that if we mean \mathop{log}\nolimits to base, say, 10 we write {\mathop{log}\nolimits }_{10}(x), i.e., if y ={\mathop{ log}\nolimits }_{10}(x), x = 1{0}^{y}.

It may help you to remember that a logarithm tries to extract a power from a number, e.g. the {\mathop{log}\nolimits }_{1}0 extract the power of 10 from a number.

Change of base

Using this we can change from one base to another. Let y ={ \mathop{log}\nolimits }_{10}x, then x ={ 10}^{y}. Now let b =\mathop{ ln}\nolimits 10 (or \mathop{log}\nolimits 10), so 10 = {e}^{b}. Therefore x ={ ({e}^{b})}^{y} = {e}^{by}, so by =\mathop{ ln}\nolimits x, y = {\mathop{ln}\nolimits x\over b} = {\mathop{ln}\nolimits x\over \mathop{ln}\nolimits 10}. Hence {\mathop{log}\nolimits }_{10}x = {\mathop{ln}\nolimits x\over \mathop{ln}\nolimits 10}. Question: Determine α such that {\mathop{log}\nolimits }_{10}(x) = α{\mathop{log}\nolimits }_{2}(x).

Differential of \mathop{ln}\nolimits x

If y =\mathop{ ln}\nolimits x then

(Remember that the differential of \mathop{ln}\nolimits x is 1∕x, not the integral! This is a common error!)

Log of a product

Using the fact that {e}^{{x}_{1}}{e}^{{x}_{2}} = {e}^{{x}_{1}+{x}_{2}}, i.e., the product of exponents is the exponent of the sum, we conclude that the inverse relation holds for logarithms. Thus, the logarithm of a product is the sum of the logarithms,

Example 2.2: 

The magnitude of a start is defined as m ={\mathop{ log}\nolimits }_{10}(I∕{I}_{0}). Explain how I changes if m increase by one unit.

Solution: 

The new intensity satisfies {\mathop{log}\nolimits }_{10}({I}^{\text{new}}∕{I}_{0}) ={\mathop{ log}\nolimits }_{10}({I}^{\text{old}}∕{I}_{0}) + 1. Using the properties of the logarithms, we find that

\eqalignno{ {\mathop{log}\nolimits }_{10}({I}^{\text{new}}∕{I}_{0}) & ={\mathop{ log}\nolimits }_{10}({I}^{\text{old}}∕{I}_{0}) +{\mathop{ log}\nolimits }_{10}10 & & \cr {\mathop{log}\nolimits }_{10}({I}^{\text{new}}∕{I}_{0}) & ={\mathop{ log}\nolimits }_{10}(10{I}^{\text{old}}∕{I}_{0}) & & \cr ({I}^{\text{new}}∕{I}_{0}) & = (10{I}^{\text{old}}∕{I}_{0}) & & \cr {I}^{\text{new}} & = 10{I}^{\text{old}} & & }

Example 2.3: 

An unresolved doube-star has magnitude 7. Find the individual magnitudes, assuming that both stars have the same one.

Solution: 

Since intensities add up, we have 7 ={\mathop{ log}\nolimits }_{10}(2I∕{I}_{0}) ={\mathop{ log}\nolimits }_{10}(2) +{\mathop{ log}\nolimits }_{1}0(I∕{I}_{0}) ={\mathop{ log}\nolimits }_{10}(2) + m. Thus we conclude that m = 7 −{\mathop{ log}\nolimits }_{10}(2) = 6.69897.