2.2 Trigonometric functions

Figure 2.3: A plot of the sine and cosine.

Figure 2.4: A plot of the tangent and cotangent.

Figure 2.5: A plot of the secans and cosecans.

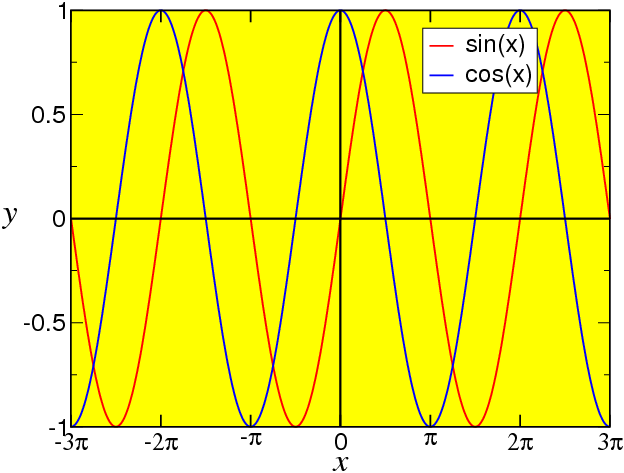
Trigonometric functions are the sine (\mathop{sin}\nolimits (x)), cosine (\mathop{cos}\nolimits (x)), tangent (\mathop{tan}\nolimits (x) =\mathop{ sin}\nolimits (x)∕\mathop{cos}\nolimits (x)), cotangent (\mathop{cot}\nolimits (x) = 1∕\mathop{tan}\nolimits (x)), secans (\mathop{sec}\nolimits (x) = 1∕\mathop{cos}\nolimits (x)) and cosecans (\mathop{cosec}\nolimits (x) = 1∕\mathop{sin}\nolimits (x)).

2.2.1 Trigonometric identities

We shall assume that you are familiar with the sine and cosine of the sum of two angles,

We also expect you to know that

for all θ. Substitute A = B in Eq. (2.8), and find \mathop{sin}\nolimits 2A =\mathop{ sin}\nolimits A\mathop{cos}\nolimits A +\mathop{ cos}\nolimits A\mathop{sin}\nolimits A, and thus

In (2.9) put B = A, \mathop{cos}\nolimits 2A =\mathop{ cos}\nolimits A\mathop{cos}\nolimits A −\mathop{ sin}\nolimits A\mathop{sin}\nolimits A, so

Example 2.4: 

Evaluate \mathop{cos}\nolimits (75∘).

Solution: 

\begin{eqnarray*} \mathop{cos}\nolimits (75∘)& =& \mathop{cos}\nolimits (45∘ + 30∘) =\mathop{ cos}\nolimits 45∘\mathop{cos}\nolimits 30∘−\mathop{ sin}\nolimits 45∘\mathop{sin}\nolimits 30∘ %& \\ & =& {1\over \sqrt{2}} {\sqrt{3}\over 2} − {1\over \sqrt{2}} {1\over 2} = {\sqrt{3} − 1\over 2\sqrt{2}} = \class{boxed}{0.2588 }\quad .%&\\ \end{eqnarray*}

Note:  We shall use radians more often than degrees, 180∘ = π\text{ radians}, so

E.g., \mathop{cos}\nolimits 45∘ =\mathop{ cos}\nolimits {π\over 4} , \mathop{sin}\nolimits 30∘ =\mathop{ sin}\nolimits {π\over 6} . Usually, if there is no degree sign (∘) then the angle is specified in radians.

Example 2.5: 

Show from the equations above that

\mathop{tan}\nolimits 2A = {2\mathop{tan}\nolimits A\over 1 −{\mathop{tan}\nolimits }^{2}A}.

Hint: 

\mathop{tan}\nolimits 2A = {\mathop{sin}\nolimits 2A\over \mathop{cos}\nolimits 2A}.

Other formulae

You will sometimes need other formulae such as

(there are four of these), and

(there are three of these).

One formula you may not have seen before is

To find R and ϕ we use formula (2.8)and find

We equate the coefficient of \mathop{sin}\nolimits x and \mathop{cos}\nolimits x on both sides of the equation, and find

Therefore

and thus

We also find

so

and

({\mathop{tan}\nolimits }^{−1} will be discussed later.)

Example 2.6: 

Express 3\mathop{sin}\nolimits x + 2\mathop{cos}\nolimits x in the form R\mathop{sin}\nolimits (x + ϕ).

Solution: 

We find R\mathop{cos}\nolimits ϕ = 3, R\mathop{sin}\nolimits ϕ = 2, {R}^{2}{\mathop{ cos}\nolimits }^{2}ϕ = 9, {R}^{2}{\mathop{ sin}\nolimits }^{2}ϕ = 9 , {R}^{2}({\mathop{cos}\nolimits }^{2}ϕ +{\mathop{ sin}\nolimits }^{2}ϕ) = 9 + 4 = 13. Therefore {R}^{2} = 13, R = \sqrt{13}. Also (R\mathop{sin}\nolimits ϕ)∕(R\mathop{cos}\nolimits ϕ) = 2∕3, and thus \mathop{tan}\nolimits ϕ = 2∕3, ϕ ={\mathop{ tan}\nolimits }^{−1}(2∕3) =\mathop{ arctan}\nolimits (2∕3) = 0.588\text{ radians} = 33.7∘.

Let’s end with a physics example.

Example 2.7: 

From astronomical data tables (e.g. http://nssdc.gsfc.nasa.gov/planetary/factsheet/marsfact.html) we know that we can we can observe an apparent diameter of the planet mars between 3.5 and 25.7 arcseconds. Given the radius of the planet (3390 km), evaluate the distance of closest approach as well as the largest distance to earth.

Solution: 

This is a simple trig problem, and it helps (as always) to draw a picture, see Fig. 2.6. From that picture we see that with distance d, radius r, the angle under which we see mars satisfies \mathop{tan}\nolimits (ϕ∕2) = d∕R. Actually, for the small angles under consideration \mathop{tan}\nolimits (x) = x, if we express x in radians. Thus

d = 2R∕phi\quad .

Realizing there are 3600 arcseconds in a degree (60 second in a minute, 60 minutes in a degree), we find that we find that

d = 2R3600180∕(πphi)\quad .

Substituting the values given we find a distance of closest approach of 6.38859 × 1{0}^{7}\text{ km} and a largest distance of 4.69105 × 1{0}^{8}\text{ km}

Figure 2.6: The angle under which we see Mars.

2.2.2 Inverse Trig Functions

Figure 2.7: A plot of the inverse of the sine and cosine.

Figure 2.8: A plot of the inverse tangent and cotangent.

arcsin

The two alternative forms y ={ \mathop{sin}\nolimits }^{−1}(x) or y =\mathop{ arcsin}\nolimits (x) indicate that y is an angle whose sine is x.

Example 2.8: 

Find {\mathop{sin}\nolimits }^{−1}(1) and {\mathop{sin}\nolimits }^{−1}(1∕2).

Solution: 

y ={\mathop{ sin}\nolimits }^{−1}(1) means \mathop{sin}\nolimits (y) = 1. Therefore y = 90∘ = π∕2\text{ rads}.
y ={\mathop{ sin}\nolimits }^{−1}(1∕2) means \mathop{sin}\nolimits (y) = 1∕2, and thus y = 30∘ = π∕6\text{ rads}.

Note:  \mathop{sin}\nolimits 30∘ = 1∕2, and \mathop{sin}\nolimits 150∘ = 1∕2, and \mathop{sin}\nolimits 390∘ = 1∕2, etc., so {\mathop{sin}\nolimits }^{−1}(x) is a multivalued function. We need extra information, e.g., from the engineering situation or common sense to say which angle we are looking at.

The equation y ={\mathop{ sin}\nolimits }^{−1}(x) means the same as x =\mathop{ sin}\nolimits y, (graph of y =\mathop{ sin}\nolimits x but with axis switched), note − 1 ≤ x ≤ 1.

Note:  {\mathop{sin}\nolimits }^{−1}(x) is not the same as {1\over \mathop{sin}\nolimits x} =\mathop{ sin}\nolimits {(x)}^{−1}! The notation is very poor here but unfortunately very widely used. \mathop{arcsin}\nolimits x would be better but not too common!

arccos

Similarly y ={\mathop{ cos}\nolimits }^{−1}x =\mathop{ arccos}\nolimits x means \mathop{cos}\nolimits y = x. Once again, − 1 ≤ x ≤ 1.

arctan

y ={ \mathop{tan}\nolimits }^{−1}x =\mathop{ arctan}\nolimits x means \mathop{tan}\nolimits y = x.

Example 2.9: 

Find x given 2\mathop{cos}\nolimits x =\mathop{ sin}\nolimits x.

Solution: 

Divide by \mathop{cos}\nolimits x: 2 =\mathop{ tan}\nolimits x, or x ={\mathop{ tan}\nolimits }^{−1}(2).