6.1 Finding areas

[htb]

Figure 6.1: The surface below {x}^{2} between 1 and 3.

We have already discussed how an integral corresponds to an area.

Example 6.1: 

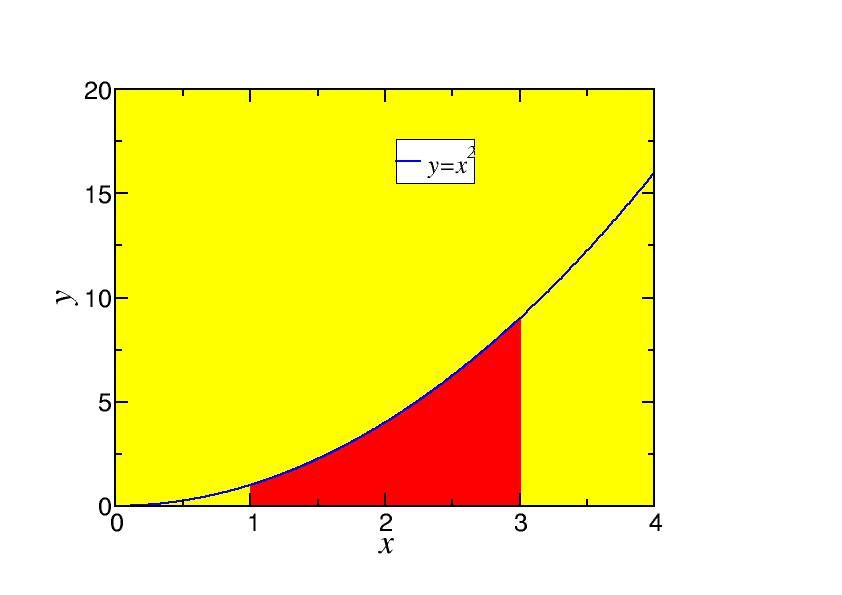
Evaluate the area A under y = {x}^{2} from x = 1 to x = 3.

Solution: 

A ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{1}^{3}{x}^{2}\kern 1.66702pt dx which is 27∕3 − 1∕3 = 26∕3, see Fig. 6.1.

6.1.1 Area between two curves

[htb]

Figure 6.2: The area between 1 − x and {e}^{x} for x between 0 and 1.

Example 6.2: 

Find the area A of the region bounded by y = {e}^{x} and y = 1 − x, for x ranging from 0 to 1, see Fig. 6.2.

Solution: 

From the graph we see that {e}^{x} is above 1 − x, so that

\begin{eqnarray*} A& =& (\text{area below $y = {e}^{x}$}) − (\text{area below $y = 1 − x$})%& \\ & =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}{e}^{x}\kern 1.66702pt dx −{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}(1 − x)\kern 1.66702pt dx %& \\ & =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}({e}^{x} − 1 + x)\kern 1.66702pt dx %& \\ & =& \bigg {({e}^{x} − x + {{x}^{2}\over 2} \bigg )}_{0}^{1} %& \\ & =& \Big (e − 1 + {1\over 2}\Big ) − 1 %& \\ & =& e − 2 + {1\over 2} %& \\ & ≈& 1.2183\quad . %& \\ \end{eqnarray*}

Here we have made the optional choice to combine the two integrands before evaluation of the integral.

6.1.2 Basic Derivation of Area Formula

Figure 6.3: Integration as the sum of area of small strips.

To find area beneath the curve y = f(x) between x = a and x = b, we divide the area into strips as shown in Fig. 6.3. Let the thickness of strip at x be δx. The height at x is f(x), and therefore the area of the strip is δA ≈ f(x)δx. Now sum up all strips from a to b. The areas is

In the limit that δx becomes infinitesimal (i.e., approaches zero), we replace δx by dx, the {\mathop{\mathop{∑ }}\nolimits }_{a}^{b} by {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{a}^{b} and so