L&T, 19.1-11
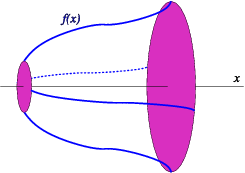
If we take area under the curve y = f(x) between x = a and x = b, as above, and then rotate it around the x axis through 360∘ we sweep out a volume called a volume of revolution V .
Again divide the area into strips of width δx. Since the height is f(x), when we rotate the strip we get a disc of radius r = f(x), see Fig. 6.5. The area of this disc is π{r}^{2} = πf{(x)}^{2}, and the volume of the disc is δV = π{r}^{2}δx. The total volume is again a sum,
|
V ={ \mathop{∑
}}_{a}^{b}π{r}^{2}δx = π{\mathop{∑
}}_{a}^{b}f{(x)}^{2}δx.
|
Now take limit where δx becomes infinitesimal, and thus
|
\class{boxed}{ V = π{\mathop{\mathop{\mathop{∫
}\nolimits }}\nolimits }_{a}^{b}f{(x)}^{2}\kern 1.66702pt dx. }
|
This is the formula for the volume of a solid of revolution.
Example 6.3:
Find the volume formed when the curve y = 1∕x, between x = 1 and x = 2 is rotated around the x axis, see Fig. 6.6
Solution:
Example 6.4:
Find the volume formed when equilateral triangle with corners at O = (0,0), A = (1,\sqrt{3}), B = (2,0) is rotated around the x axis, see Fig. 6.7.
Solution:
Along OA the curve is y = \sqrt{3}x, along AB the curve is y = 2\sqrt{3} −\sqrt{3}x. Thus