6.3 Centroids (First moment of area)

6.3.1 First moment of the area about the y axis

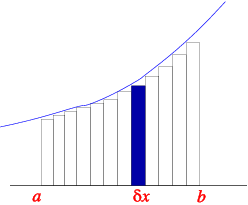
Again consider curve y = f(x) from a to b, divided into strips of thickness δx. The area of the strip is given by (δA ≈ f((x))δx). The total area is given by the sum,

If the strip is very thin then all of it is approximately at a distance x from y axis. If we now add up NOT δA but instead δA times x, i.e., δA “weighted” by x, we get the first moment of the area about the x axis,

This is usually called {M}_{x}, even though it is the first moment around the y axis.

Example 6.5: 

Find the first moment of area under y = 1 + x + {x}^{2} from x = 0 to x = 2 about the y axis.

Solution: 

\begin{eqnarray*}{ M}_{x}& =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{2}x(1 + {x}^{2} + {x}^{3})\kern 1.66702pt dx %& \\ & =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{2}(x + {x}^{2} + {x}^{3})\kern 1.66702pt dx %& \\ & =&{ \left ({x}^{2}∕2 + {x}^{3}∕3 + {x}^{4}∕4\right )}_{ 0}^{2}%& \\ & =& 2 + 8∕3 + 4 %& \\ & =& 26∕3\quad . %& \\ \end{eqnarray*}

Example 6.6: 

Find the first moment of the area under y = {e}^{−x} from x = 0 to x = 1 about the y axis.

Solution: 

{M}_{x} ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}x{e}^{−x}\kern 1.66702pt dx.

Integrate by parts: u = x, du∕dx = 1, du = dx, dv = {e}^{−x}dx. Therefore dv∕dx = {e}^{−x}, and thus v = −{e}^{−x},

\begin{eqnarray*}{ M}_{x}& =&{ \left (x{e}^{−x}\right )}_{ 0}^{1} −{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}(−{e}^{−x})\kern 1.66702pt dx%& \\ & =& −{1\over e} − 0 +{\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}{e}^{−x}\kern 1.66702pt dx %& \\ & & = −{1\over e} + {(−{e}^{−x})}_{ 0}^{1} %& \\ & =& −{1\over e} + (−{1\over e} + 1) %& \\ & =& 1 −{2\over e} = 0.2642\quad . %& \\ \end{eqnarray*}

6.3.2 First Moment of the area about the x axis

Figure 6.8: Subdividing the strips of width δx in ones of height δy.

Now consider the same strip of thickness δx. On this strip y goes from 0 to f(x). Divide strip into segments of length δy as shown in Fig. 6.8. The area of such a segment is δyδx. The total area of strip is δA ≈{\mathop{\mathop{∑ }}\nolimits }_{y=0}^{f(x)}δyδx. In the limit that δy becomes infinitesimal we get

as before. Now instead of summing segments we can weight each of them by the value of y to get

To find {M}_{y} we have to add the contributions of all strips

This is the formula for the first moment of the area about the x axis (This integral is same as that for the volume of revolution except for the factor {1\over 2} outside the integral rather than π).

Example 6.7: 

Find {M}_{y} for area under curve y = 1 + x + {x}^{2} from x = 0 to x = 2 (same area as in example xxxx(1))

Solution: 

\begin{eqnarray*} f(x)& =& 1 + x + {x}^{2}\quad , %& \\ {f(x)}^{2}& =&{ (1 + x + {x}^{2})}^{2} %& \\ & =& 1 + 2x + 3{x}^{2} + 2{x}^{3} + {x}^{4}\quad .%& \\ \end{eqnarray*}

Therefore

\begin{eqnarray*}{ M}_{y}& =& {1\over 2}{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{2}(1 + 2x + 3{x}^{2} + 2{x}^{3} + {x}^{4})\kern 1.66702pt dx%& \\ & =& {1\over 2}\bigg {(x + {x}^{2} + {x}^{3} + {{x}^{4}\over 2} + {{x}^{5}\over 5} \bigg )}_{0}^{2} %& \\ & =& {1\over 2}\Big (2 + 4 + 8 + 8 + {32\over 5} \Big ) %& \\ & =& 11 + {16\over 5} %& \\ & =& {71\over 5} %& \\ & =& 14.2\quad . %& \\ \end{eqnarray*}

6.3.3 Centroid of a plane area

Example 6.8: 

Find the centroid of the area under y = 1 + x + {x}^{2} from x = 0 to x = 2 using the previous two examples.

Solution: 

We know that {M}_{x} = 26∕3 and {M}_{y} = 71∕5, and we just need to determine A,

\begin{eqnarray*} A& =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{2}(1 + x + {x}^{2})\kern 1.66702pt dx %& \\ & =& {(x + {x}^{2}∕2 + {x}^{3}∕3)}_{ 0}^{2}%& \\ & =& 2 + 2 + 8∕3 %& \\ & =& 20∕3\quad . %& \\ \end{eqnarray*}

Therefore

\begin{eqnarray*}{ x}_{C}& =& {{M}_{x}\over A} = {3\over 20} {26\over 3} = {26\over 20} = 1.3\quad , %& \\ {y}_{C}& =& {{M}_{y}\over A} = {3\over 20} {71\over 5} = {213\over 100} = 2.13\quad .%& \\ \end{eqnarray*}

6.3.4 Meaning of the centroid

If we have thin plate with constant thickness then the centroid is the position of centre of mass (C of M). The C of M is the point at which all mass can be regarded as acting. Let mass per unit area be ρ: This will be constant if the thickness is constant (and material is of uniform composition). The total mass m = Aρ where A is area. Turning effect about y axis of mass m at (x,y) would be mx = Aρx. A strip of thickness δx, height f(x) has area f(x)δx. Mass would be ρf(x)δx. Total turning effect is {\mathop{\mathop{∑ }}\nolimits }_{a}^{b}xρf(x)δx →{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{a}^{b}xf(x)dx = ρ{M}_{x}, therefore Aρx = ρ{M}_{x}, therefore {x}_{C} = 1∕A{M}_{x}.