2.3 Polar Coordinates

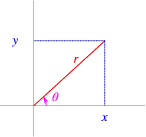
The position of any point P in two-dimensional space can be specified by giving its (x,y) coordinates. However we could also say where P is by giving the distance from the origin 0, and the direction we need to go.

Figure 2.9: The meaning of polar coordinates.

These two quantities are the polar coordinates (r,θ) of P. From a right angled triangle we see that r\mathop{cos}\nolimits θ = x, and r\mathop{sin}\nolimits θ = y, so {x}^{2} + {y}^{2} = {r}^{2}{\mathop{cos}\nolimits }^{2}θ + {r}^{2}{\mathop{sin}\nolimits }^{2}θ = {r}^{2}, and thus r = \sqrt{{x}^{2 } + {y}^{2}}. (N.B. We always take positive square root here!) Also {y\over x} = {r\mathop{ sin}\nolimits θ\over r\mathop{ cos}\nolimits θ} =\mathop{ tan}\nolimits θ, Therefore θ ={ \mathop{tan}\nolimits }^{−1}(y∕x). In this case we must always draw a diagram. The reason is that two different angles can have the same tangent. The only relevant once for polar coordinates are that \mathop{tan}\nolimits {θ}_{1} =\mathop{ tan}\nolimits {θ}_{2}, when {θ}_{2} = 180∘ + {θ}_{1} = π + {θ}_{1}. If P is in first or second quadrant we use {θ}_{1}, and if P is in third or fourth quadrant we use {θ}_{2}. So always draw a little sketch!

Example 2.10: 

Find the polar coordinates corresponding to x = −1,y = −1.

Solution: 

r = \sqrt{{1}^{2 } + {1}^{2}} = \sqrt{2}, and \mathop{tan}\nolimits θ = y∕x = {−1\over −1} = 1. From the sketch we see that θ = 225∘ = {5π\over 4}

---

Figure 2.10: A sketch of (-1,-1) and polar coordinates.

---

2.3.1 Polar curves

Often we wish to draw curves in polar coordinates; the most important example are the Kepler orbits, the ones resulting from a particle moving in the gravitational fiels of a single orbit, e.g., a single planet/comet orbiting the sun.

The Kepler orbits can be shown to take the form

Here {R}_{0} is a quantity with unit length, determined from masses and gravitational parameters. We now use this relation (with ϕ' = 0, for simplicity) to find the typical orbits for ϵ = 0, |ϵ| < 1 (we shall choose − 1∕2), |ϵ| = 1, and |ϵ| > 1 (we shall choose 2).

In order to plot these results we rewrite the relation as

and plot the value of r for each ϕ (or a suitably chosen selection).

ϵ = 0

This is a circle.

ϵ = −1∕2

Figure 2.11: The Keplerian ellipse obtained for ϵ = −1∕2.

In this case it is not very hard to solve the problem: All values of ϕ give a positive r, and the easiest solution is just to plot a suitable large number of values. Obvious choices are ϕ = 0,π∕6,π∕4,π∕3,π∕2,\mathop{\mathop{…}}, and these immediately lead to the elliptical structure shown in Fig. 2.11. It can be shown that this is a real ellipse, with the origin (the sun around which the palnet revolves) as one of the focusses of the ellipse.

ϵ = 1

Figure 2.12: The Keplerian parabola obtained for ϵ = 1.

In this case we cannot use ϕ = π, and we thus conclude that the curve moves away to infinity. Once again we can draw a large number of points and we find a parabola, see Fig. 2.12.

ϵ = 2

Figure 2.13: The range where r is positive for ϵ = 2.

Figure 2.14: The Keplerian hyperbola obtained for ϵ = 2.

We need to carefully find the allowed range for ϕ, see Fig. 2.13, and we conclude that − 2π∕2 < ϕ < 2π∕3. Near the end points r diverges, and we can actually expand the value of r in the behaviour near these two points (Callenge question: how?) to find the two asymptotes y = ±\left (2∕\sqrt{3} −\sqrt{3}x\right ), which as we can see from Fig. 2.14 are indeed correct. The curve obtained is a hyperbola.