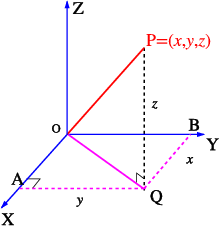
Figure 3.1: 3d geometry
In a 3-dimensional world we have to consider 3-dimensional coordinate geometry rather than 2-dimensional.
First of all we set up a set of 3 mutually orthogonal coordinate axes, usually labeled x, y and z, see Fig. 3.1.
The z of axis is called right-handed, using the cork-screw rule: when rotating from x to y the z-axis is in the up direction. We can specify any point p by its coordinates (x,y,z). From 2D geometry we know that O{Q}^{2} = {x}^{2} + {y}^{2}. Thus
If we call, as is conventional, OP = r, then
|
\class{boxed}{ {r}^{2} = {x}^{2} + {y}^{2} + {z}^{2}. }
|