3.2 Vectors and vector arithmetic

3.2.1 What is a vector?

In order to understand what a vector is we must distinguish carefully between: Scalars: These are specified by (i) their units, and (ii) the number of units. Together we refer to this as their magnitude. Examples are length, density, time, temperature, speed, etc. Vectors: These are specified by (i) their units, (ii) the number of units and (iii) a direction. Examples are velocity, acceleration, force, heat flux, etc.

A short word about notation: we shall use the notation \overrightarrow{AB} for a vector pointing from A to B, and a for an abstract vector. These notations do not agree with Stroud, but are standard practice! For handwriting, where we cannot write a boldface letter, we shall use an underline (\underline{a} = a) to denote the boldface.

3.2.2 Graphical representation

Figure 3.2: A vector represented by a directed line segment

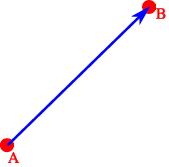
We often represent a vector by a line-segment pointing from a point A to a point B, so that it has both direction an length, see Fig. 3.2. The length of the segment AB gives the magnitude and the arrow specifies the direction. The vector \overrightarrow{AB} is often called a displacement vector, since, unlike an abstract vector, it has a begin- and end-point. We say that the displacement vector \overrightarrow{AB} represents the abstract vector a if the direction and magnitude agree.

3.2.3 Equality and line of action

Figure 3.3: The representatives of two equal vectors.

Two vectors {F}_{1} and {F}_{2} are equal if they have the same magnitude (including units!) and direction, even if their representatives do not act along the same line, see Fig. 3.3: A vector can be moved parallel to itself without changing its value.

The line along which the vector points is called the line of action.

3.2.4 Negative of a vector

Figure 3.4: The negative of a vector.

We shall often use the negative of a vector. The vector −F is defined as a vector of the same magnitude as F, but pointing in the opposite direction, see Fig. 3.4. If F is represented by \overrightarrow{AB}, or loosely (i.e., equality denotes “is represented by”) F =\overrightarrow{ AB}, then −F =\overrightarrow{ BA}.

3.2.5 magnitude of a vector

We use as special notation for the magnitude: AB, |\overrightarrow{AB}| or |a| or a. This is a scalar describing the length of the vector, and is therefore always positive. It does carry the same units, however.

3.2.6 Multiplication by a scalar

Figure 3.5: A vector, and twice the same vector.

Given a scalar a and a vector F, then aF is a vector of the magnitude |a|F and the same direction as F if a is positive, and oposite to F if a is negative, see Fig. 3.5. Thus 1 ⋅F = F, − 1 ⋅F = −F.

3.2.7 Unit vectors

Unit vectors have magnitude 1 (they are dimensionless, i.e., mathematical objects). We often define unit vectors associated with a physical vector. If n is a unit vector in the direction of a vector F, then, using our laws of mutiplication, the vector F = Fn, since the factors on both sides have the same direction and magnitude. From this we learn that

a relation used frequently.