Warning: jsMath
requires JavaScript to process the mathematics on this page.
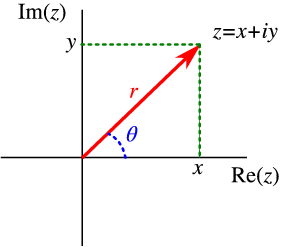
1.2 1.2.1 A complex number z = x + iy has two
real components: the real part \text{Re}(z) = x
and the imaginary part \text{Im}(z) = y .
Let us write them in the form of a 2D vector, cf. Fig. 1.1 .
\begin{eqnarray}
z = x + iy ↔ r = (x,y).& & %&(1.16) \\
\end{eqnarray}
Polar Form: Any complex number z = x + iy can be
written in polar form, (remember that r = (r\mathop{cos}\nolimits θ,r\mathop{sin}\nolimits θ)
in polar coordinates)
\begin{eqnarray}
z& =& x + iy = r\mathop{cos}\nolimits (θ) + ir\mathop{sin}\nolimits (θ)%&
\\
x& =& r\mathop{cos}\nolimits (θ),\quad y = r\mathop{sin}\nolimits (θ) %&
\\
r& =& \sqrt{{x}^{2 } + {y}^{2}} = \sqrt{z\bar{z}} %&
\\
\mathop{tan}\nolimits (θ)& =& {y\over
x} ⇝ θ =\mathop{ arctan}\nolimits \left ({y\over
x}\right ). %&(1.17) \\
\end{eqnarray}
1.2.2 The length of the vector r = (x,y)
representing the complex number z = x + iy ,
\begin{eqnarray}
|z| := r = \sqrt{{x}^{2 } + {y}^{2}} = \sqrt{z\bar{z}}& & %&(1.18) \\
\end{eqnarray}
is called modulus of z .
The angle θ ,
\begin{eqnarray}
\mathop{arg}\nolimits (z) := θ =\mathop{ arctan}\nolimits \left ({y\over
x}\right )& & %&(1.19) \\
\end{eqnarray}
is called the argument of z .
The angle θ is usually
restricted to − π < θ ≤ π , even though
any interval of length 2π will
do, and we sometimes use 0 ≤ θ < 2π .
1.2.3 Addition:
\begin{eqnarray}
(x,y)& ↔& z = x + iy %&
\\
({x}_{1},{y}_{1}) + ({x}_{2},{y}_{2}) = ({x}_{1} + {x}_{2},{y}_{1} + {y}_{2})& ↔& {z}_{1} + {z}_{2} = ({x}_{1} ± {x}_{2}) + i({y}_{1} ± {y}_{2}).%&(1.20) \\
\end{eqnarray}
Therefore, we have to add the vectors representing the complex numbers.
Complex Conjugate:
\begin{eqnarray}
z& =& x + iy = r\mathop{cos}\nolimits (θ) + ir\mathop{sin}\nolimits (θ) ⇝ %&
\\
\bar{z}& =& x − iy = r\mathop{cos}\nolimits (θ) − ir\mathop{sin}\nolimits (θ) = r\mathop{cos}\nolimits (−θ) + ir\mathop{sin}\nolimits (−θ).%&(1.21) \\
\end{eqnarray}
The angle becomes negative: check what this means geometrically!
Multiplication:
\begin{eqnarray}
{z}_{1}& =& {r}_{1}\mathop{ cos}\nolimits ({θ}_{1}) + i{r}_{1}\mathop{ sin}\nolimits ({θ}_{1}),\quad {z}_{2} = {r}_{2}\mathop{ cos}\nolimits ({θ}_{2}) + i{r}_{2}\mathop{ sin}\nolimits ({θ}_{2}) ⇝ %&
\\
{z}_{1}{z}_{2}& =& {r}_{1}{r}_{2}[\mathop{cos}\nolimits ({θ}_{1})\mathop{cos}\nolimits ({θ}_{2}) −\mathop{ sin}\nolimits ({θ}_{1})\mathop{sin}\nolimits ({θ}_{2})] + i{r}_{1}{r}_{2}[\mathop{cos}\nolimits ({θ}_{1})\mathop{sin}\nolimits ({θ}_{2}) +\mathop{ sin}\nolimits ({θ}_{1})\mathop{cos}\nolimits ({θ}_{2})]%&
\\
& =& {r}_{1}{r}_{2}[\mathop{cos}\nolimits ({θ}_{1} + {θ}_{2}) + i\mathop{sin}\nolimits ({θ}_{1} + {θ}_{2})] %&(1.22) \\
\end{eqnarray}
This means that
\begin{eqnarray}
|{z}_{1}{z}_{2}| = |{z}_{1}||{z}_{2}|,\quad \mathop{arg}\nolimits ({z}_{1}{z}_{2}) =\mathop{ arg}\nolimits ({z}_{1}) +\mathop{ arg}\nolimits ({z}_{2}).& & %&(1.23) \\
\end{eqnarray}
Try to sketch an example for this in the x − y
diagram for yourself!
1.2.4 Let us differentiate a complex number of unit modulus,
z =\mathop{ cos}\nolimits θ + i\mathop{sin}\nolimits θ w.r.t.
θ .
{d\over
dθ}(\mathop{cos}\nolimits θ + i\mathop{sin}\nolimits θ) = −\mathop{sin}\nolimits θ + i\mathop{cos}\nolimits θ = i(\mathop{cos}\nolimits θ + i\mathop{sin}\nolimits θ).
(1.24)
In short,
This suggests that we can write z
as z = {e}^{iθ} . We
shall construct further proof the consistency of this suggestion (which can also be used to define the complex
exponent) below.
1.2.5 We can easily generalise the multiplication of two complex numbers in polar form to calculcate an arbitrary power
of z ,
{z}^{n} (integer
n ):
\begin{eqnarray}
z& =& r[\mathop{cos}\nolimits (θ) + i\mathop{sin}\nolimits (θ)] ⇝ %&
\\
{z}^{2}& =& {r}^{2}[\mathop{cos}\nolimits (2θ) + i\mathop{sin}\nolimits (2θ)] ⇝ %&
\\
{z}^{3}& =& z{z}^{2} = {r}^{3}[\mathop{cos}\nolimits (3θ) + i\mathop{sin}\nolimits (3θ)] ⇝ %&
\\
& \mathop{\mathop{⋮}}& %&(1.26)
\\
{z}^{n}& =& {r}^{n}[\mathop{cos}\nolimits (nθ) + i\mathop{sin}\nolimits (nθ)] ⇝ %&
\\
& & %&(1.27) \\
\end{eqnarray}
Since {z}^{n} = {r}^{n}{[\mathop{cos}\nolimits (θ) + i\mathop{sin}\nolimits (θ)]}^{n} ,
this means
\begin{eqnarray}{
[\mathop{cos}\nolimits (θ) + i\mathop{sin}\nolimits (θ)]}^{n} =\mathop{ cos}\nolimits (nθ) + i\mathop{sin}\nolimits (nθ)& & %&(1.28) \\
\end{eqnarray}
which is a useful equation for proving trigonometric identities; it is also useful for doing many integrals that occur
in physics.
Example:
\begin{eqnarray}
{[\mathop{cos}\nolimits (θ) + i\mathop{sin}\nolimits (θ)]}^{2}& =& [\mathop{cos}\nolimits (2θ) + i\mathop{sin}\nolimits (2θ)] ⇔ %&
\\
{\mathop{cos}\nolimits }^{2}(θ) −{\mathop{ sin}\nolimits }^{2}(θ) + 2i\mathop{cos}\nolimits (θ)\mathop{sin}\nolimits (θ)& =& \mathop{cos}\nolimits (2θ) + i\mathop{sin}\nolimits (2θ) ⇒ %&
\\
\mathop{cos}\nolimits (2θ) ={\mathop{ cos}\nolimits }^{2}(θ) −{\mathop{ sin}\nolimits }^{2}(θ)& , & \quad \mathop{sin}\nolimits (2θ) = 2\mathop{cos}\nolimits (θ)\mathop{sin}\nolimits (θ).%&(1.29) \\
\end{eqnarray}
Clearly, this is entirely consistent with the properties of the exponent:
{({e}^{iθ})}^{n} = {({e}^{a})}^{b} with
a = iθ and
b = n is
{e}^{ab} = {e}^{inθ} .