[back][up]

5.5 Eigenvalues and eigenvectors

In understanding the nature of a matrix (or really the linear transformation represented by it) we often would like to understand those vectors that are transformed into themselves, i.e., where

Ae = λe,\qquad \text{($λ$ is a constant).}
(5.37)

This equation is called the “eigenvalue problem”; λ is called an eigenvalue and e an eigenvector.

The question is now, obviously, how to determine λ and e. By using a simple trick, we can solve for λ without having to know e. To this end we write

λx = λIx = \left (\array{ λ&0\cr 0 &λ } \right )x,

and we can thus rewrite the eigenvalue problem as

(A − λI)x = 0.
(5.38)

We have argued in the previous section that this has only the trivial solution if \mathop{det}(A − λI)\mathrel{≠}0, i.e., x = 0. In order to avoid this we must require

\mathop{det}(A − λI) = 0\quad .
(5.39)

For a two-by-two matrix this is a simple quadratic equation.

Example 5.1: 

Find the eigenvalues and eigenvectors of A = \left (\array{ 1&2\cr 2 &1} \right ).

Solution: 

\begin{eqnarray*} \mathop{det}(A − λI)& =& \left |\array{ 1 − λ&2 \cr 2 &1 − λ} \right |%& \\ & =& {(1 − λ)}^{2} − 4 = 0 %&\\ \end{eqnarray*}

Solutions are λ = 1 ± 2 = −1,3.

Now determine the eigenvalues by solving (A − λI)e = 0. For {λ}_{1} = −1 we find

\left (\array{ 2&2\cr 2 &2} \right )\left (\array{ {e}_{1} \cr {e}_{2} } \right ) = 0

and thus {e}_{1} = −{e}_{2}, and {e}^{(1)} = c\left (\array{ 1\cr 1} \right ). The arbitrary constant can be chosen at will. Some standard choices are 1 (simple), 1∕\sqrt{2} (length 1), etc.

The same algebra for the other eigenvalue leads to {e}^{(2)} = d\left (\array{ 1\cr − 1} \right ).

If we rewrite

\left (\array{ x\cr y } \right ) = (x+y)∕2\left (\array{ 1\cr 1 } \right )+(x−y)∕2\left (\array{ 1\cr − 1} \right ),

we can easily understand the importantce of the eigenvectors:

A\left (\array{ x\cr y } \right ) = 3(x+y)∕2\left (\array{ 1\cr 1 } \right )−(x−y)∕2\left (\array{ 1\cr − 1} \right ).

Thus the component parallel to (1,1) is stretches by a factor of 3, and the component parallel to (−1,1) is inverted (multiplied by − 1).

5.5.1 A physics example

The most important physical example of the role of the eigenvalue problem can be found in the case of coupled oscillators.

coupled

Figure 5.1: Two coupled oscillators.

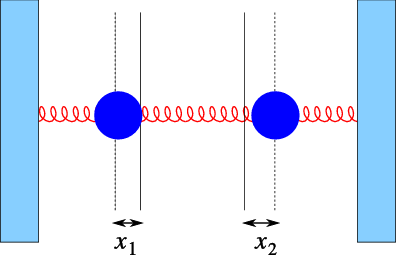
Consider Fig. 5.1. There we show the case of two masses, coupled by three springs. We assume that {x}_{1} and {x}_{2} are the distances of the masses from the equilibrium position. At that point we assume the strings are untentioned (neither stretched nor compressed).

The equations of motion take a simple form

\begin{eqnarray*}{ m}_{1}\ddot{{x}}_{1}& =& −{k}_{1}{x}_{1} + {k}_{2}({x}_{2} − {x}_{1}) = −({k}_{1} + {k}_{2}){x}_{1} + {k}_{2}{x}_{2}%& \\ {m}_{2}\ddot{{x}}_{2}& =& −{k}_{3}{x}_{2} − {k}_{2}({x}_{2} − {x}_{1}) = −({k}_{3} + {k}_{2}){x}_{2} + {k}_{2}{x}_{1}%& \\ \end{eqnarray*}

We now take the masses equal ({m}_{1} = {m}_{2} = m), and all the spring constants equal as well ({k}_{1} = {k}_{2} = {k}_{3} = m{ω}^{2}. We then find that

\begin{eqnarray*} \ddot{x} = {ω}^{2}\left (\array{ − 2& 1 \cr 1 & − 2 } \right )x& & %&\\ \end{eqnarray*}

This equation can now be solved by writing the standard exponential form, x = e{e}^{zt}. We then get

\begin{eqnarray*}{ z}^{2}e = {ω}^{2}\left (\array{ − 2& 1 \cr 1 & − 2 } \right )e& & %&\\ \end{eqnarray*}

Which is an eigenvalue problem. Write {z}^{2} = {ω}^{2}λ, and we find that λ = −1,−3. Thus z = ±iω,±i\sqrt{3}ω. The eigenvectors for these two eigenvalues are (1,1) and (1,−1), respectively.

Thus, in all its generality, we find using superposition that

x = \left (\array{ 1\cr 1 } \right )(A\mathop{cos}\nolimits (ωt)+B\mathop{sin}\nolimits (ωt))+\left (\array{ 1\cr − 1 } \right )(C\mathop{cos}\nolimits (\sqrt{3}ωt)+D\mathop{sin}\nolimits (\sqrt{3}ωt)).
(5.40)

This general motion thus consists of the superposition of motion of the two masses in phase ({x}_{1} = {x}_{2}, with frequency ω) and one maximally out of phase ({x}_{1} = −{x}_{1}, with frequency \sqrt{3}ω).

[back][up]