[forward][back][up]

4.6 Fourier series for even and odd functions

Notice that in the Fourier series of the square wave (4.23) all coefficients {a}_{n} vanish, the series only contains sines. This is a very general phenomenon for so-called even and odd functions.

A function is called even if f(−x) = f(x), e.g. \mathop{cos}\nolimits (x).
A function is called odd if f(−x) = −f(x), e.g. \mathop{sin}\nolimits (x).

These have somewhat different properties than the even and odd numbers:

  1. The sum of two even functions is even, and of two odd ones odd.
  2. The product of two even or two odd functions is even.
  3. The product of an even and an odd function is odd.

Question: Which of the following functions is even or odd?
a) \mathop{sin}\nolimits (2x), b) \mathop{sin}\nolimits (x)\mathop{cos}\nolimits (x), c) \mathop{tan}\nolimits (x), d) {x}^{2}, e) {x}^{3}, f) |x|

Answer: even: d, f; odd: a, b, c, e.

Now if we look at a Fourier series, the Fourier cosine series

f(x) = {{a}_{0}\over 2} +{ \mathop{∑ }}_{n=1}^{∞}{a}_{ n}\mathop{ cos}\nolimits {nπ\over L} x
(4.28)

describes an even function (why?), and the Fourier sine series

f(x) ={ \mathop{∑ }}_{n=1}^{∞}{b}_{ n}\mathop{ sin}\nolimits {nπ\over L} x
(4.29)

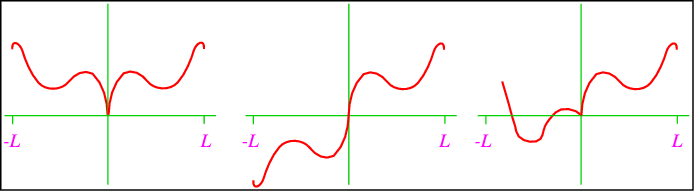
an odd function. These series are interesting by themselves, but play an especially important rôle for functions defined on half the Fourier interval, i.e., on [0,L] instead of [−L,L]. There are three possible ways to define a Fourier series in this way, see Fig. 4.2

  1. Continue f as an even function, so that f'(0) = 0.
  2. Continue f as an odd function, so that f(0) = 0.
  3. Neither of the two above. We now nothing about f at x = 0.

even-odd


Figure 4.2: A sketch of the possible ways to continue f beyond its definition region for 0 < x < L. From left to right as even function, odd function or assuming no symmetry at all.

Of course these all lead to different Fourier series, that represent the same function on [0,L]. The usefulness of even and odd Fourier series is related to the imposition of boundary conditions. A Fourier cosine series has df∕dx = 0 at x = 0, and the Fourier sine series has f(x = 0) = 0. Let me check the first of these statements:

{d\over dx}\left [{{a}_{0}\over 2} +{ \mathop{∑ }}_{n=1}^{∞}{a}_{ n}\mathop{ cos}\nolimits {nπ\over L} x\right ] = −{π\over L}{\mathop{∑ }}_{n=1}^{∞}n{a}_{ n}\mathop{ sin}\nolimits {nπ\over L} x = 0\quad \text{at $x = 0$.}
(4.30)

triangle


Figure 4.3: The function y = 1 − x.

As an example look at the function f(x) = 1 − x, 0 ≤ x ≤ 1, with an even continuation on the interval [−1,1]. We find

\begin{eqnarray} {a}_{0}& =& {2\over 1}{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}(1 − x)dx = 1 %& \\ {a}_{n}& =& 2{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{1}(1 − x)\mathop{cos}\nolimits nπxdx %& \\ & =&{ \left .\left \{ {2\over nπ}\mathop{sin}\nolimits nπx − {2\over { n}^{2}{π}^{2}}[\mathop{cos}\nolimits nπx + nπx\mathop{sin}\nolimits nπx]\right \}\right |}_{0}^{1} %& \\ & =& \left \{\array{ 0 \quad &\text{if $n$ even}\cr {4\over { n}^{2}{π}^{2}} \quad &\text{if $n$ is odd} } \right .\quad .%&(4.31)\\ \end{eqnarray}

So, changing variables by defining n = 2m + 1 so that in a sum over all m n runs over all odd numbers,

f(x) = {1\over 2} + {4\over { π}^{2}}{ \mathop{∑ }}_{m=0}^{∞} {1\over { (2m + 1)}^{2}}\mathop{ cos}\nolimits (2m + 1)πx.
(4.32)

[forward][back][up]