Warning: jsMath
requires JavaScript to process the mathematics on this page.
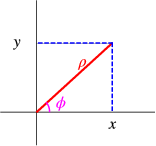
7.1 Polar coordinates in two dimensions are defined by
\begin{eqnarray}
x = ρ\mathop{cos}\nolimits ϕ,y = ρ\mathop{sin}\nolimits ϕ,& & %&(7.1)
\\
ρ = \sqrt{{x}^{2 } + {y}^{2}},ϕ =\mathop{ arctan}\nolimits (y∕x),& & %&(7.2) \\
\end{eqnarray}
as indicated schematically in Fig. 7.1 .
Using the chain rule we find
\begin{eqnarray}
{∂\ \over
∂x}& =& {∂ρ\over
∂x} {∂\ \over
∂ρ} + {∂ϕ\over
∂x} {∂\ \over
∂ϕ} %&
\\
& =& {x\over
ρ} {∂\ \over
∂ρ} − {y\over {
ρ}^{2}} {∂\ \over
∂ϕ} %&
\\
& =& \mathop{cos}\nolimits ϕ {∂\ \over
∂ρ} −{\mathop{sin}\nolimits ϕ\over
ρ} {∂\ \over
∂ϕ},%&(7.3)
\\
{∂\ \over
∂y}& =& {∂ρ\over
∂y} {∂\ \over
∂ρ} + {∂ϕ\over
∂y} {∂\ \over
∂ϕ} %&
\\
& =& {y\over
ρ} {∂\ \over
∂ρ} + {x\over {
ρ}^{2}} {∂\ \over
∂ϕ} %&
\\
& =& \mathop{sin}\nolimits ϕ {∂\ \over
∂ρ} + {\mathop{cos}\nolimits ϕ\over
ρ} {∂\ \over
∂ϕ},%&(7.4) \\
\end{eqnarray}
We can write
\begin{eqnarray}
\mathop{∇}& =&{ \hat{e}}_{ρ} {∂\ \over
∂ρ} +\hat{{ e}}_{ϕ}{1\over
ρ} {∂\ \over
∂ϕ}%&(7.5) \\
\end{eqnarray}
where the unit vectors
\begin{eqnarray}
\hat{{e}}_{ρ}& =& (\mathop{cos}\nolimits ϕ,\mathop{sin}\nolimits ϕ), %&
\\
\hat{{e}}_{ϕ}& =& (−\mathop{sin}\nolimits ϕ,\mathop{cos}\nolimits ϕ),%&(7.6) \\
\end{eqnarray}
are an orthonormal set. We say that circular coordinates are orthogonal .
We can now use this to evaluate {\mathop{∇}}^{2} ,
\begin{eqnarray}{
\mathop{∇}}^{2}& =& {\mathop{cos}\nolimits }^{2}ϕ {{∂}^{2}\ \over
∂{ρ}^{2}} + {\mathop{sin}\nolimits ϕ\mathop{cos}\nolimits ϕ\over
{ρ}^{2}} {∂\ \over
∂ϕ} + {{\mathop{sin}\nolimits }^{2}ϕ\over
ρ} {∂\ \over
∂ρ} + {{\mathop{sin}\nolimits }^{2}ϕ\over
{ρ}^{2}} {{∂}^{2}\ \over
∂{ϕ}^{2}} + {\mathop{sin}\nolimits ϕ\mathop{cos}\nolimits ϕ\over
{ρ}^{2}} {∂\ \over
∂ϕ} %&
\\
& & +{\mathop{sin}\nolimits }^{2}ϕ {{∂}^{2}\ \over
∂{ρ}^{2}} −{\mathop{sin}\nolimits ϕ\mathop{cos}\nolimits ϕ\over
{ρ}^{2}} {∂\ \over
∂ϕ} + {{\mathop{cos}\nolimits }^{2}ϕ\over
ρ} {∂\ \over
∂ρ} + {{\mathop{cos}\nolimits }^{2}ϕ\over
{ρ}^{2}} {{∂}^{2}\ \over
∂{ϕ}^{2}} −{\mathop{sin}\nolimits ϕ\mathop{cos}\nolimits ϕ\over
{ρ}^{2}} {∂\ \over
∂ϕ}%&(7.7)
\\
& =& {{∂}^{2}\ \over
∂{ρ}^{2}} + {1\over
ρ} {∂\ \over
∂ρ} + {1\over {
ρ}^{2}} {{∂}^{2}\ \over
∂{ϕ}^{2}} %&
\\
& =& {1\over
ρ} {∂\ \over
∂ρ}\left (ρ {∂\ \over
∂ρ}\right ) + {1\over {
ρ}^{2}} {{∂}^{2}\ \over
∂{ϕ}^{2}}. %&
\\
& & %&(7.8) \\
\end{eqnarray}
A final useful relation is the integration over these coordinates.
As indicated schematically in Fig. 7.2 , the surface related to a change
ρ → ρ + δρ ,
ϕ → ϕ + δϕ is
ρδρδϕ . This leads us to the conclusion
that an integral over x,y
can be rewritten as
{\mathop{\mathop{\mathop{∫
}\nolimits }}\nolimits }_{V }f(x,y)dxdy ={\mathop{ \mathop{\mathop{∫
}\nolimits }}\nolimits }_{V }f(ρ\mathop{cos}\nolimits ϕ,ρ\mathop{sin}\nolimits ϕ)ρdρdϕ
(7.9)