Warning: jsMath
requires JavaScript to process the mathematics on this page.
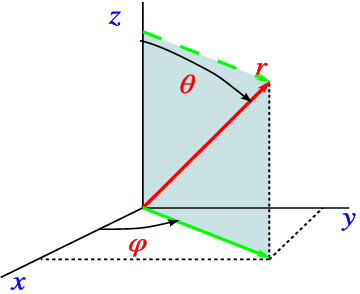
7.2 Spherical coordinates are defined as
\begin{eqnarray}
x = r\mathop{cos}\nolimits ϕ\mathop{sin}\nolimits θ,\kern 2.77695pt y = r\mathop{sin}\nolimits ϕ\mathop{sin}\nolimits θ,\kern 2.77695pt z = r\mathop{cos}\nolimits θ,& & %&(7.10)
\\
r = \sqrt{{x}^{2 } + {y}^{2 } + {z}^{2}},\kern 2.77695pt ϕ =\mathop{ arctan}\nolimits (y∕x),\kern 2.77695pt θ =\mathop{ arctan}\nolimits \left ({\sqrt{{x}^{2 } + {y}^{2}}\over
z} \right ),& & %&(7.11) \\
\end{eqnarray}
as indicated schematically in Fig. 7.3 .
Using the chain rule we find
\begin{eqnarray}
{∂\ \over
∂x}& =& {∂r\over
∂x} {∂\ \over
∂r} + {∂ϕ\over
∂x} {∂\ \over
∂ϕ} + {∂θ\over
∂x} {∂\ \over
∂θ} %&
\\
& =& {x\over
r} {∂\ \over
∂r} − {y\over {
x}^{2} + {y}^{2}} {∂\ \over
∂ϕ} + {xz\over {
r}^{2}\sqrt{{x}^{2 } + {y}^{2}}} {∂\ \over
∂θ} %&
\\
& =& \mathop{sin}\nolimits θ\mathop{cos}\nolimits ϕ {∂\ \over
∂r} − {\mathop{sin}\nolimits ϕ\over
r\mathop{sin}\nolimits θ} {∂\ \over
∂ϕ} + {\mathop{cos}\nolimits ϕ\mathop{cos}\nolimits θ\over
r} {∂\ \over
∂θ},%&(7.12)
\\
{∂\ \over
∂y}& =& {∂r\over
∂y} {∂\ \over
∂r} + {∂ϕ\over
∂y} {∂\ \over
∂ϕ} + {∂θ\over
∂y} {∂\ \over
∂θ} %&
\\
& =& {y\over
r} {∂\ \over
∂r} + {x\over {
x}^{2} + {y}^{2}} {∂\ \over
∂ϕ} + {yz\over {
r}^{2}\sqrt{{x}^{2 } + {y}^{2}}} {∂\ \over
∂θ} %&
\\
& =& \mathop{sin}\nolimits θ\mathop{sin}\nolimits ϕ {∂\ \over
∂r} + {\mathop{cos}\nolimits ϕ\over
r\mathop{sin}\nolimits θ} {∂\ \over
∂ϕ} + {\mathop{sin}\nolimits ϕ\mathop{cos}\nolimits θ\over
r} {∂\ \over
∂θ}, %&(7.13)
\\
{∂\ \over
∂z}& =& {∂r\over
∂z} {∂\ \over
∂r} + {∂ϕ\over
∂z} {∂\ \over
∂ϕ} + {∂θ\over
∂z} {∂\ \over
∂θ} %&
\\
& =& {z\over
r} {∂\ \over
∂r} −{\sqrt{{x}^{2 } + {y}^{2}}\over
{r}^{2}} {∂\ \over
∂θ} %&
\\
& =& \mathop{sin}\nolimits θ\mathop{sin}\nolimits ϕ {∂\ \over
∂r} −{\mathop{sin}\nolimits θ\over
r} {∂\ \over
∂θ}. %&(7.14)
\\
& & %&(7.15) \\
\end{eqnarray}
once again we can write \mathop{∇}
in terms of these coordinates.
\begin{eqnarray}
\mathop{∇}& =& \hat{{e}}_{r} {∂\ \over
∂r} +\hat{{ e}}_{ϕ} {1\over
r\mathop{sin}\nolimits θ} {∂\ \over
∂ϕ} +\hat{{ e}}_{θ}{1\over
r} {∂\ \over
∂θ}%&(7.16) \\
\end{eqnarray}
where the unit vectors
\begin{eqnarray}
\hat{{e}}_{r}& =& (\mathop{sin}\nolimits θ\mathop{cos}\nolimits ϕ,\mathop{sin}\nolimits θ\mathop{sin}\nolimits ϕ,\mathop{cos}\nolimits θ), %&
\\
\hat{{e}}_{ϕ}& =& (−\mathop{sin}\nolimits ϕ,\mathop{cos}\nolimits ϕ,0), %&
\\
\hat{{e}}_{θ}& =& (\mathop{cos}\nolimits ϕ\mathop{cos}\nolimits θ,\mathop{sin}\nolimits ϕ\mathop{cos}\nolimits θ,−\mathop{sin}\nolimits θ).%&(7.17) \\
\end{eqnarray}
are an orthonormal set. We say that spherical coordinates are orthogonal .
We can use this to evaluate Δ ={ \mathop{∇}}^{2} ,
Δ = {1\over {
r}^{2}} {∂\ \over
∂r}\left ({r}^{2} {∂\ \over
∂r}\right ) + {1\over {
r}^{2}} {1\over
\mathop{sin}\nolimits θ} {∂\ \over
∂θ}\left (\mathop{sin}\nolimits θ {∂\ \over
∂θ}\right ) + {1\over {
r}^{2}} {{∂}^{2}\ \over
∂{ϕ}^{2}}
(7.18)
Finally, for integration over these variables we need to know the volume of the small cuboid contained between
r and
r + δr ,
θ and
θ + δθ and
ϕ and
ϕ + δϕ . The length of the sides due
to each of these changes is δr ,
rδθ and
r\mathop{sin}\nolimits θδθ ,
respectively. We thus conclude that
{\mathop{\mathop{\mathop{∫
}\nolimits }}\nolimits }_{V }f(x,y,z)dxdydz ={\mathop{ \mathop{\mathop{∫
}\nolimits }}\nolimits }_{V }f(r,θ,ϕ){r}^{2}\mathop{ sin}\nolimits θdrdθdϕ.
(7.19)