[forward][up]

8.1 Example

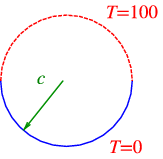
Consider a circular plate of radius c\text{ m}, insulated from above and below. The temperature on the circumference is 10{0}^{∘}\ \text{C} on half the circle, and {0}^{∘}\ \text{C} on the other half.

circ˙T


Figure 8.1: The boundary conditions for the temperature on a circular plate.

The differential equation to solve is

{ρ}^{2}{{∂}^{2}u\over ∂{ρ}^{2}} + ρ{∂u\over ∂ρ} + {{∂}^{2}u\over ∂{ϕ}^{2}} = 0,
(8.1)

with boundary conditions

u(c,ϕ) = \left \{\array{ 100\quad &\text{if $0 < ϕ < π$}\cr 0 \quad &\text{if $π < ϕ < 2π$} } \right .\quad .
(8.2)

8.1.1 Periodic BC

There is no real boundary in the ϕ direction, but we introduce one, since we choose to let ϕ run from 0 to 2π only. So what kind of boundary conditions do we apply? We would like to see “seamless behaviour”, which specifies the periodicity of the solution in ϕ,

\begin{eqnarray} u(ρ,ϕ + 2π)& =& u(ρ,ϕ), %&(8.3) \\ {∂u\over ∂ϕ}(ρ,ϕ + 2π)& =& {∂u\over ∂ϕ}(ρ,ϕ).%&(8.4) \\ \end{eqnarray}

If we choose to put the seem at ϕ = −π we have the periodic boundary conditions

\begin{eqnarray} u(ρ,2π)& =& u(ρ,0), %&(8.5) \\ {∂u\over ∂ϕ}(ρ,2π)& =& {∂u\over ∂ϕ}(ρ,0).%&(8.6) \\ \end{eqnarray}

We separate variables, and take, as usual

u(ρ,ϕ) = R(ρ)Φ(ϕ).
(8.7)

This gives the usual differential equations

\begin{eqnarray} Φ'' − λΦ& =& 0,%&(8.8) \\ {ρ}^{2}R'' + ρR' + λR& =& 0.%&(8.9) \\ \end{eqnarray}

Our periodic boundary conditions gives a condition on Φ,

Φ(0) = Φ(2π),\kern 2.77695pt \kern 2.77695pt Φ'(0) = Φ'(2π).
(8.10)

The other boundary condition involves both R and Φ.

[forward][up]