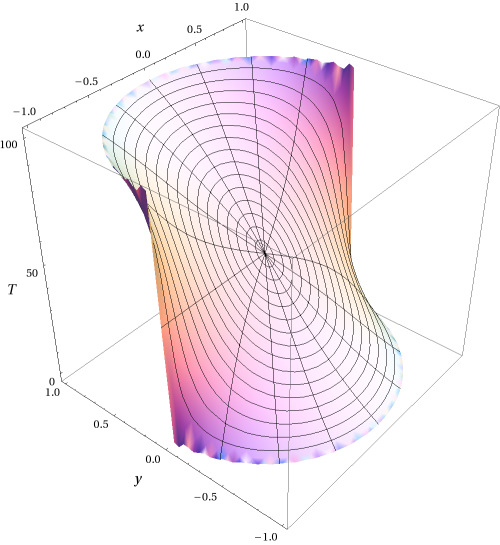
Figure 8.2: The temperature (8.31)
In summary, we have
|
u(ρ,ϕ) = {{A}_{0}\over
2} +{ \mathop{∑
}}_{n=1}^{∞}{ρ}^{n}\left ({A}_{
n}\mathop{ cos}\nolimits nϕ + {B}_{n}\mathop{ sin}\nolimits nϕ\right ).
| (8.28) |
The one remaining boundary condition can now be used to determine the coefficients {A}_{n} and {B}_{n},
We find
In summary
|
u(ρ,ϕ) = 50 + {200\over
π} {\mathop{∑
}}_{n\ odd}{\left ({ρ\over
c}\right )}^{n}{\mathop{sin}\nolimits nϕ\over
n} .
| (8.31) |
We clearly see the dependence of u on the pure number r∕c, rather than ρ. A three dimensional plot of the temperature is given in Fig. 8.2.