Figure 10.3: A plot of the first three Bessel functions {J}_{n}
and {Y }_{n}.
Bessel’s equation of order ν is given by
|
{x}^{2}y'' + xy' + ({x}^{2} − {ν}^{2})y = 0.
| (10.6) |
Clearly x = 0 is a regular singular point, so we can solve by Frobenius’ method. The indicial equation is obtained from the lowest power after the substitution y = {x}^{γ}, and is
|
{γ}^{2} − {ν}^{2} = 0
| (10.7) |
So a generalised series solution gives two independent solutions if ν\mathrel{≠}{1\over 2}n. Now let us solve the problem and explicitly substitute the power series,
|
y = {x}^{ν}{ \mathop{∑
}}_{n}{a}_{n}{x}^{n}.
| (10.8) |
From Bessel’s equation we find
|
{\mathop{∑
}}_{n}(n + ν)(n + ν − 1){a}_{ν}{x}^{m+ν} +{ \mathop{∑
}}_{n}(n + ν){a}_{ν}{x}^{m+ν} +{ \mathop{∑
}}_{n}({x}^{2} − {ν}^{2}){a}_{
ν} = 0
| (10.9) |
which leads to
|
[{(m + ν)}^{2} − {ν}^{2}]{a}_{
m} = −{a}_{m−2}
| (10.10) |
or
|
{a}_{m} = − {1\over
m(m + 2ν)}{a}_{m−2}.
| (10.11) |
If we take ν = n > 0, we have
|
{a}_{m} = − {1\over
m(m + 2n)}{a}_{m−2}.
| (10.12) |
This can be solved by iteration,
If we choose1 {a}_{0} = {1\over n!{2}^{n}} we find the Bessel function of order n
|
{J}_{n}(x) ={ \mathop{∑
}}_{k=0}^{∞} {{(−1)}^{k}\over
k!(k + n)!}{\left ({x\over
2}\right )}^{2k+n}.
| (10.14) |
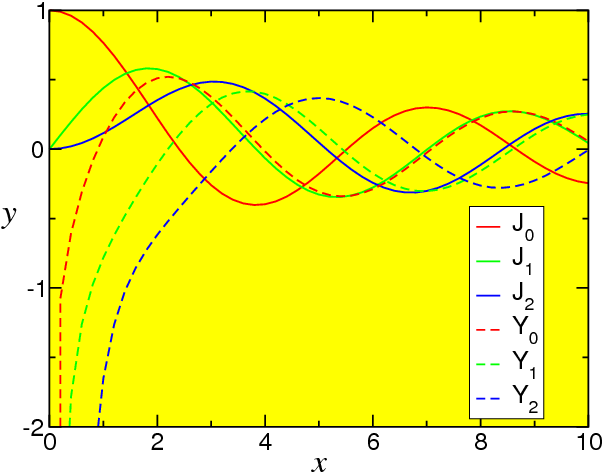
There is another second independent solution (which should have a logarithm in it) with goes to infinity at x = 0.
The general solution of Bessel’s equation of order n is a linear combination of J and Y ,
|
y(x) = A{J}_{n}(x) + B{Y }_{n}(x).
| (10.15) |