[forward][back][up]

10.3 Gamma function

For ν not an integer the recursion relation for the Bessel function generates something very similar to factorials. These quantities are most easily expressed in something called a Gamma-function, defined as

Γ(ν) ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−t}{t}^{ν−1}dt,\kern 2.77695pt \kern 2.77695pt \kern 2.77695pt ν > 0.
(10.16)

Some special properties of Γ function now follow immediately:

\begin{eqnarray} Γ(1)& =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−t}dt ={ \left .−{e}^{−1}\right |}_{ 0}^{∞} = 1 − {e}^{−∞} = 1%& \\ Γ(ν)& =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−t}{t}^{ν−1}dt = −{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{d{e}^{−t}\over dt} {t}^{ν−1}dt %& \\ & =&{ \left .−{e}^{−t}{t}^{ν−1}\right |}_{ 0}^{∞} + (ν − 1){\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−t}{t}^{ν−2}dt%&(10.17) \\ \end{eqnarray}

The first term is zero, and we obtain

Γ(ν) = (ν − 1)Γ(ν − 1)
(10.18)

From this we conclude that

Γ(2) = 1 ⋅ 1 = 1,\kern 2.77695pt Γ(3) = 2 ⋅ 1 ⋅ 1 = 2,\kern 2.77695pt Γ(4) = 3 ⋅ 2 ⋅ 1 ⋅ 1 = 2,\kern 2.77695pt Γ(n) = (n − 1)!.
(10.19)

Thus for integer argument the Γ function is nothing but a factorial, but it also defined for other arguments. This is the sense in which Γ generalises the factorial to non-integer arguments. One should realize that once one knows the Γ function between the values of its argument of, say, 1 and 2, one can evaluate any value of the Γ function through recursion. Given that Γ(1.65) = 0.9001168163 we find

Γ(3.65) = 2.65 × 1.65 × 0.9001168163 = 3.935760779.
(10.20)

Question: Evaluate Γ(3), Γ(11), Γ(2.65).

Answer: 2! = 2, 10! = 3628800, 1.65 × 0.9001168163 = 1.485192746.

We also would like to determine the Γ function for ν < 1. One can invert the recursion relation to read

Γ(ν − 1) = {Γ(ν)\over ν − 1},
(10.21)

Γ(0.7) = Γ(1.7)∕0.7 = 0.909∕0.7 = 1.30.

What is Γ(ν) for ν < 0? Let us repeat the recursion derived above and find

Γ(−1.3) = {Γ(−0.3)\over −1.3} = {Γ(0.7)\over −1.3 ×−0.3} = {Γ(1.7)\over 0.7 ×−0.3 ×−1.3} = 3.33\kern 2.77695pt .
(10.22)

This works for any value of the argument that is not an integer. If the argument is integer we get into problems. Look at Γ(0). For small positive ϵ

Γ(±ϵ) = {Γ(1 ± ϵ)\over ±ϵ} = ±{1\over ϵ} →±∞.
(10.23)

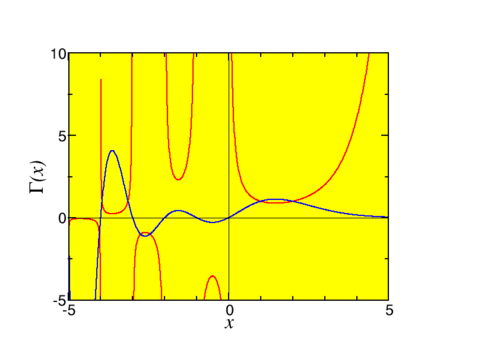
Thus Γ(n) is not defined for n ≤ 0. This can be easily seen in the graph of the Γ function, Fig. 10.4.

Gamma


Figure 10.4: A graph of the Γ function (solid line). The inverse 1∕Γ is also included (dashed line). Note that this last function is not discontinuous.

Finally, in physical problems one often uses Γ(1∕2),

Γ({1\over 2}) ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−t}{t}^{−1∕2}dt = 2{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−t}d{t}^{1∕2} = 2{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−{x}^{2} }dx.
(10.24)

This can be evaluated by a very smart trick, we first evaluate Γ{(1∕2)}^{2} using polar coordinates

\begin{eqnarray} Γ{({1\over 2})}^{2}& =& 4{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−{x}^{2} }dx{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{e}^{−{y}^{2} }dy %& \\ & =& 4{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{π∕2}{e}^{−{ρ}^{2} }ρdρdϕ = π.%&(10.25) \\ \end{eqnarray}

(See the discussion of polar coordinates in Sec. 7.1.) We thus find

Γ(1∕2) = \sqrt{π},\kern 2.77695pt \kern 2.77695pt Γ(3∕2) = {1\over 2}\sqrt{π},\kern 2.77695pt \kern 2.77695pt etc.
(10.26)

[forward][back][up]