[forward][back][up]

10.7 Our initial problem and Bessel functions

We started the discussion from the problem of the temperature on a circular disk, solved in polar coordinates, Since the initial conditions do not depend on ϕ, we expect the solution to be radially symmetric as well, u(ρ,t), which satisfies the equation

\begin{eqnarray} {∂u\over ∂t} & =& k\left [{{∂}^{2}u\over ∂{ρ}^{2}} + {1\over ρ} {∂u\over ∂ρ}\right ],%& \\ u(c,t)& =& 0, %& \\ u(ρ,0)& =& f(ρ). %&(10.60) \\ \end{eqnarray}

With u(ρ,t) = R(ρ)T(t) we found the equations

\begin{eqnarray}{ ρ}^{2}R'' + ρR' + λ{ρ}^{2}R& =& 0\kern 2.77695pt \kern 2.77695pt \kern 2.77695pt \kern 2.77695pt R(c) = 0%& \\ T' + λkT = 0.& & %&(10.61) \\ \end{eqnarray}

The equation for R is clearly self-adjoint, it can be written as

[ρR']' + λρR = 0
(10.62)

So how does the equation for R relate to Bessel’s equation? Let us make the change of variables x = \sqrt{λ}ρ. We find

{d\over dρ} = \sqrt{λ} {d\over dx},
(10.63)

and we can remove a common factor \sqrt{λ} to obtain (X(x) = R(ρ))

[xX']' + xX = 0,
(10.64)

which is Bessel’s equation of order 0, i.e.,

R(ρ) = {J}_{0}(ρ\sqrt{λ}).
(10.65)

The boundary condition R(c) = 0 shows that

c\sqrt{{λ}_{n}} = {x}_{n},
(10.66)

where {x}_{n} are the points where {J}_{0}(x) = 0. We thus conclude

{R}_{n}(ρ) = {J}_{0}(ρ\sqrt{{λ}_{n}}).
(10.67)

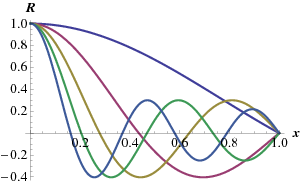
the first five solutions {R}_{n} (for c = 1) are shown in Fig. 10.5.

BesselZero


Figure 10.5: A graph of the first five functions {R}_{n}

From Sturm-Liouville theory we conclude that

{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{∞}ρdρ\kern 1.66702pt {R}_{ n}(ρ){R}_{m}(ρ) = 0\kern 2.77695pt \kern 2.77695pt if\ n\mathrel{≠}m.
(10.68)

Together with the solution for the T equation,

{T}_{n}(t) =\mathop{ exp}\nolimits (−{λ}_{n}kt)
(10.69)

we find a Fourier-Bessel series type solution

u(ρ,t) ={ \mathop{∑ }}_{n=1}^{∞}{A}_{ n}{J}_{0}(ρ\sqrt{{λ}_{n}})\mathop{exp}\nolimits (−{λ}_{n}kt),
(10.70)

with {λ}_{n} = {({x}_{n}∕c)}^{2}.

In order to understand how to determine the coefficients {A}_{n} from the initial condition u(ρ,0) = f(ρ) we need to study Fourier-Bessel series in a little more detail.

[forward][back][up]