[back][up]

11.4 Modelling the eye–revisited

Let me return to my model of the eye. With the functions {P}_{n}(\mathop{cos}\nolimits θ) as the solution to the angular equation, we find that the solutions to the radial equation are

R = A{r}^{n} + B{r}^{−n−1}.
(11.36)

The singular part is not acceptable, so once again we find that the solution takes the form

u(r,θ) ={ \mathop{∑ }}_{n=0}^{∞}{A}_{ n}{r}^{n}{P}_{ n}(\mathop{cos}\nolimits θ)
(11.37)

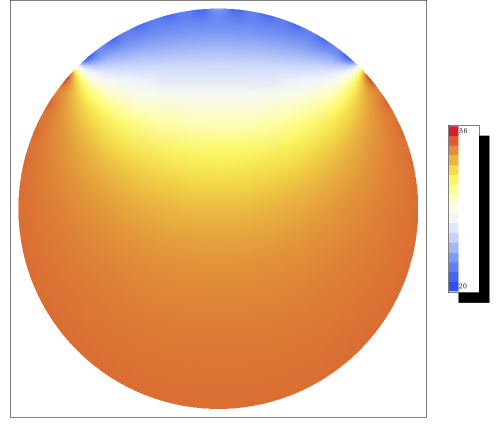
We now need to impose the boundary condition that the temperature is 2{0}^{∘} C in an opening angle of 4{5}^{∘}, and 3{6}^{∘} elsewhere. This leads to the equation

\begin{eqnarray} {\mathop{∑ }}_{n=0}^{∞}{A}_{ n}{c}^{n}{P}_{ n}(\mathop{cos}\nolimits θ) = \left \{\array{ 20&0 < θ < π∕4 \cr 36&π∕4 < θ < π } \right .& & %&(11.38)\\ \end{eqnarray}

This leads to the integral, after once again changing to x =\mathop{ cos}\nolimits θ,

{A}_{n} = {2n + 1\over 2} \left [{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−1}^{1}36{P}_{ n}(x)dx −{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{{1\over 2} \sqrt{2}}^{1}16{P}_{ n}(x)dx\right ].
(11.39)

These integrals can easily be evaluated, and a sketch for the temperature can be found in figure 11.3.

eye


Figure 11.3: A cross-section of the temperature in the eye. We have summed over the first 40 Legendre polynomials.

Notice that we need to integrate over x =\mathop{ cos}\nolimits θ to obtain the coefficients {A}_{n}. The integration over θ in spherical coordinates is {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{0}^{π}\mathop{ sin}\nolimits θdθ ={\mathop{ \mathop{\mathop{∫ }\nolimits }}\nolimits }_{−1}^{1}1dx, and so automatically implies that \mathop{cos}\nolimits θ is the right variable to use, as also follows from the orthogonality of {P}_{n}(x).

[back][up]