[forward][back][up]

10.4 Simple example

The best way to clarify this abstract discussion is to consider the quantum mechanics of the Harmonic oscillator of mass m and frequency ω,

\hat{H} = −{{ℏ}^{2}\over 2m} {{d}^{2}\over d{x}^{2}} + {1\over 2}m{ω}^{2}{x}^{2}.
(10.8)

If we assume that the wave function at time t = 0 is a linear superposition of the first two eigenfunctions,

\begin{eqnarray} ψ(x,t = 0)& =& \sqrt{{1\over 2}}{ϕ}_{0}(x) −\sqrt{{1\over 2}}{ϕ}_{1}(x), %& \\ {ϕ}_{0}(x)& =&{ \left ({mω\over πℏ} \right )}^{1∕4}\mathop{ exp}\nolimits \left (−{mω\over 2ℏ} {x}^{2}\right ), %& \\ {ϕ}_{1}(x)& =&{ \left ({mω\over πℏ} \right )}^{1∕4}\mathop{ exp}\nolimits \left (−{mω\over 2ℏ} {x}^{2}\right )\sqrt{ {mω\over ℏ}} x.%&(10.9) \\ \end{eqnarray}

(The functions {ϕ}_{0} and {ϕ}_{1} are the normalised first and second states of the harmonic oscillator, with energies {E}_{0} = {1\over 2}ℏω and {E}_{1} = {3\over 2}ℏω.) Thus we now kow the wave function for all time:

\begin{eqnarray} ψ(x,t)& =& \sqrt{{1\over 2}}{ϕ}_{0}(x){e}^{−{1\over 2}iωt} −\sqrt{{1\over 2}}{ϕ}_{1}(x){e}^{−{3\over 2}iωt}.%&(10.10) \\ \end{eqnarray}

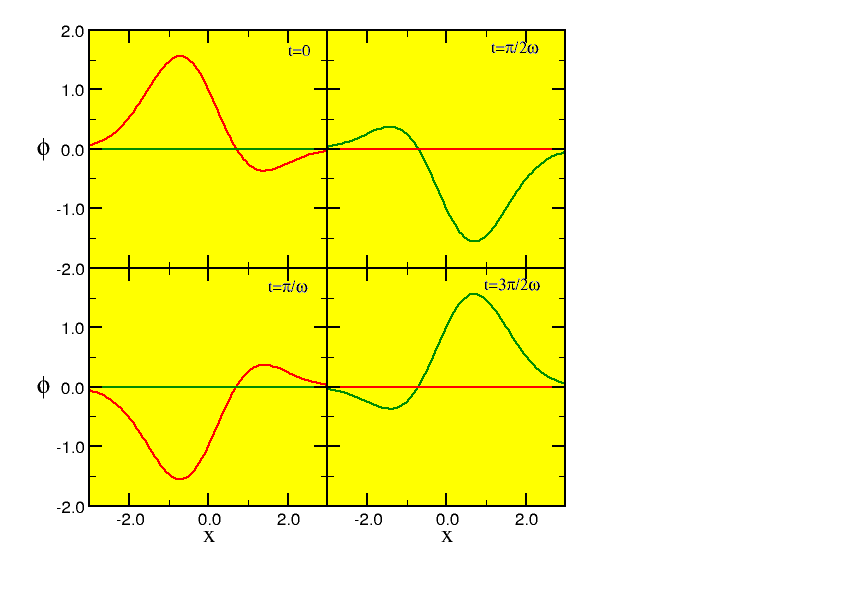
In figure 10.1 we plot this quantity for a few times.

timedep1


Figure 10.1: The wave function (10.10) for a few values of the time t. The solid line is the real part, and the dashed line the imaginary part.

The best way to visualize what is happening is to look at the probability density,

\begin{eqnarray} P(x,t)& =& ψ{(x,t)}^{∗}ψ(x,t) %& \\ & =& {1\over 2}\left ({ϕ}_{0}{(x)}^{2} + {ϕ}_{ 1}{(x)}^{2} − 2{ϕ}_{ 0}(x){ϕ}_{1}(x)\mathop{cos}\nolimits ωt\right ).%&(10.11) \\ \end{eqnarray}

This clearly oscillates with frequency ω.

Question: Show that {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}P(x,t)dx = 1.

Another way to look at that is to calculate the expectation value of \hat{x}:

\begin{eqnarray} \langle \hat{x}\rangle & =& {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}P(x,t)dx %& \\ & =& {1\over 2}{\underbrace{ {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{ϕ}_{ 0}{(x)}^{2}xdx}}_{ =0} + {1\over 2}{\underbrace{ {\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{ϕ}_{ 1}{(x)}^{2}xdx}}_{ =0} −\mathop{ cos}\nolimits ωt{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{ϕ}_{ 0}(x){ϕ}_{1}(x)xdx%& \\ & =& −\mathop{cos}\nolimits ωt\sqrt{ {ℏ\over mω}} {1\over \sqrt{π}}{\mathop{\mathop{\mathop{∫ }\nolimits }}\nolimits }_{−∞}^{∞}{y}^{2}{e}^{−{y}^{2} } %& \\ & =& −{1\over 2}\sqrt{ {ℏ\over mω}}\mathop{cos}\nolimits ωt. %&(10.12) \\ \end{eqnarray}

This once again exhibits oscillatory behaviour!

[forward][back][up]