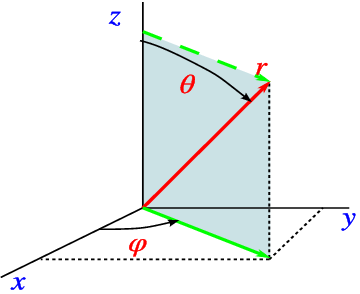
[forward][back][up]

11.2 Spherical coordinates

The solution to Schrödinger’s equation in three dimensions is quite complicated in general. Fortunately, nature lends us a hand, since most physical systems are “rotationally invariant”, i.e., V (x) depends on the size of x, but not its direction! In that case it helps to introduce spherical coordinates, as denoted in Fig. 11.1.

spherical


Figure 11.1: The spherical coordinates r, θ, φ.

The coordinates r, θ and ϕ are related to the standard ones by

\begin{eqnarray} x& =& r\mathop{cos}\nolimits φ\mathop{sin}\nolimits θ%& \\ y& =& r\mathop{sin}\nolimits φ\mathop{sin}\nolimits θ%& \\ \ & =& r\mathop{cos}\nolimits θ %&(11.6) \\ \end{eqnarray}

where 0 < r < ∞, 0 < θ < π and 0 < ϕ < 2π. In these new coordinates we have

Δf(r,θ,φ) = {1\over { r}^{2}} {∂\over ∂r}\left ({r}^{2} {∂\over ∂r}f(r,θ,φ)\right ) − {1\over { r}^{2}}\left [ {1\over \mathop{sin}\nolimits θ} {∂\over ∂θ}\left (\mathop{sin}\nolimits θ {∂\over ∂θ}f(r,θ,φ)\right ) + {{∂}^{2}\over ∂{φ}^{2}}f(r,θ,φ)\right ].
(11.7)

[forward][back][up]