To be used in future
 Section 4.5: Coupling of light to atoms and nuclei: multipole couplings Up Chapter 4: Charged Particles and Electromagnetic Fields Section 4.7: The Pauli-Schrödinger equation 

4.6 Internal degrees of freedom: spin

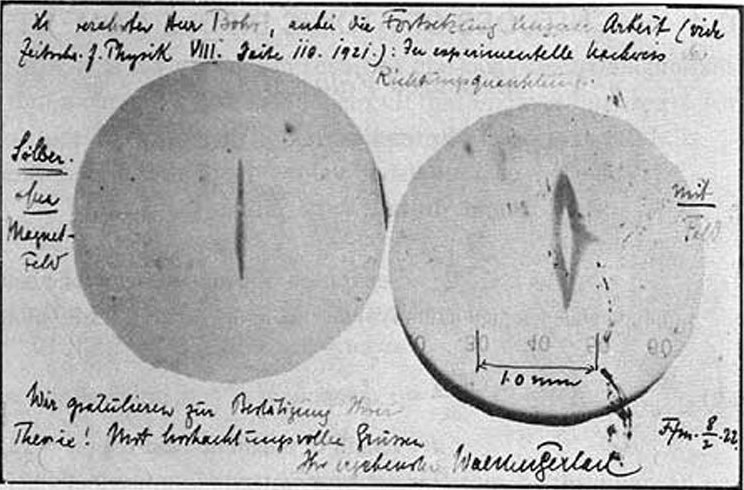
Up to this stage we have not looked at internal degrees of freedom, but from the famous Stern-Gerlach experiment↓ (particles with spin in a magnetic field), see Figs. 4.2↓,4.3↓, we know that the internal spin degree of freedom interacts in interesting ways with the magnetic field.
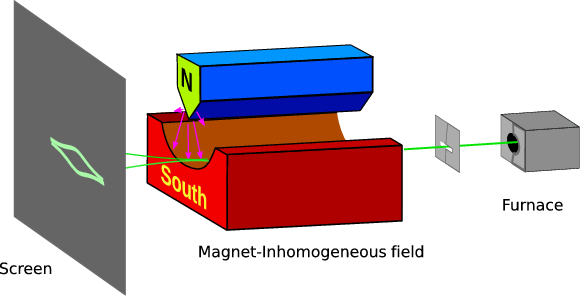
figure Figures/SternGerlach.png
Figure 4.2 A sketch of the Stern-Gerlach apparatus. The asymmetric choice of magnets gives the slight structure seen in Fig.4.3↓.
figure Figures/sternGerlach.jpg
Figure 4.3 Gerlach’s postcard, dated 8 February 1922, to Niels Bohr. It shows a photograph of the beam splitting, with the message “....the experimental proof of directional quantisation. We congratulate you on the confirmation of your theory....” (Physics Today December 2003)
The effect can be described in an ad-hoc way by assuming that the spin degree of freedom (an angular momentum with magnitude ) is aligned by the magnetic field,. This is described by adding a term to the Hamiltonian. Here we have used the empirical value of the Bohr magneton↓, which we will derive now from first principles.
 Section 4.5: Coupling of light to atoms and nuclei: multipole couplings Up Chapter 4: Charged Particles and Electromagnetic Fields Section 4.7: The Pauli-Schrödinger equation