3.3 Vector Addition

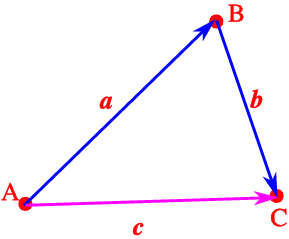
Addition of vectors is achieved by moving the starting point of the second vector to coincide with the endpoint of the first.

3.3.1 Triangle Law

Figure 3.6: Addition of two vectors

Thus, as shown in Fig. 3.6 the displacement vectors are aligned, and we have \overrightarrow{AB} +\overrightarrow{ BC} =\overrightarrow{ AC}. If the displacements represent a, b, and c, respectively we see that a + b = c, or “changing sides” c = a + b. This is called the triangle law of addition. It is used by always drawing displacement vectors that connect in the order of the addition. I.e., in the addition above the endpoint of the representative of a coinides with the start point of the vector b. The sum vector is often called the resultant.

3.3.2 Parallelogram Law

Figure 3.7: order of addition of two vectors

If we investigate both a + b and b + a, as shown in Fig. 3.7, we discover that the displacement vectors form the four sides of a parallelogram (parallelogram law), as well as the fact that the order of addition doesn’t matter (commutativity):

3.3.3 General Addition

Figure 3.8: Addition of several vectors

If we wish to add several vectors, we repeat the procedure sketched for two vectors, putting all of them end to beginning, \overrightarrow{AB} +\overrightarrow{ BC} +\overrightarrow{ CD} +\overrightarrow{ DE} +\overrightarrow{ EF} =\overrightarrow{ AF}.

3.3.4 Associativity

Figure 3.9: Associativity of addition

For number we know that they have the associative property, (a + b) + c = a + (b + c). Let us investigate graphically whether such a relation holds for vectors. As we see from Fig. 3.9, this can be written in terms of displacement vectors as \overrightarrow{AC} +\overrightarrow{ CD} =\overrightarrow{ AB} +\overrightarrow{ CD}, an obvious truth.

3.3.5 Closed sets of vectors: null vector

Figure 3.10: a closed set of vectors

If we add together a set of vectors that returns to the starting point (a closed set of vectors), see Fig. 3.10, \overrightarrow{AB} +\overrightarrow{ BC} +\overrightarrow{ CA} =\overrightarrow{ AA} = 0, we get a zero length vector (the null vector, see below).

3.3.6 Subtraction of vectors

If we subtract two vectors, we reverse the one with the minus sign (i.e., reverse the direction of the arrow on that vector) and use the rules for addition, a−b = a + (−b).

3.3.7 Zero or Null Vector

In subtraction if b = a then a−a = 0 (zero or null vector). All null vectors are regarded as equal with zero magnitude but no natural direction. 0 + a = a + 0 = a for any vector a.