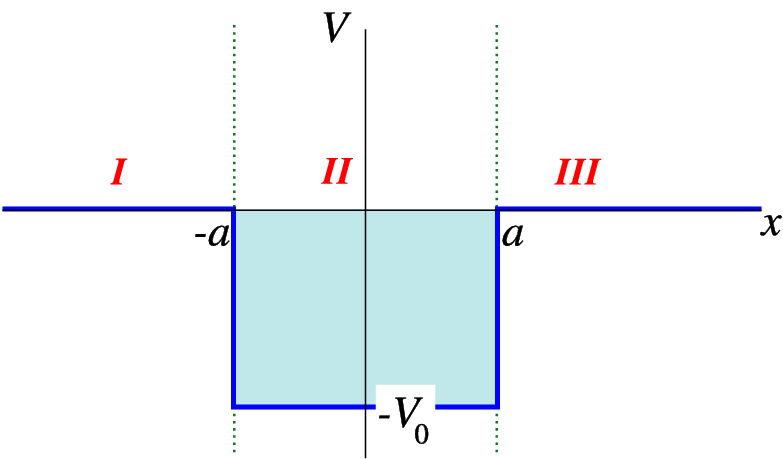
One of the simplest potentials to study the properties of is the so-called square well potential,
|
V = \left \{\array{
0 &|x| > a\cr
− {V }_{
0}&|x| < a } \right ..
| (4.1) |
We define three areas, from left to right I, II and III. In areas I and III we have the Schrödinger equation
|
−{{ℏ}^{2}\over
2m} {{d}^{2}\over
d{x}^{2}}ψ(x) = Eψ(x)
| (4.2) |
whereas in area II we have the equation
|
−{{ℏ}^{2}\over
2m} {{d}^{2}\over
d{x}^{2}}ψ(x) = (E + {V }_{0})ψ(x)
| (4.3) |
__________________________________________________________________
. In this class we shall quite often encounter the ordinary differential equations
|
{{d}^{2}\over
d{x}^{2}}f(x) = −{α}^{2}f(x)
| (4.4) |
which has as solution
|
f(x) = {A}_{1}\mathop{ cos}\nolimits (αx) + {B}_{1}\mathop{ sin}\nolimits (αx) = {C}_{1}{e}^{iαx} + {D}_{
1}{e}^{−iαx},
| (4.5) |
and
|
{{d}^{2}\over
d{x}^{2}}g(x) = +{α}^{2}g(x)
| (4.6) |
which has as solution
|
g(x) = {A}_{2}\mathop{ cosh}\nolimits (αx) + {B}_{2}\mathop{ sinh}\nolimits (αx) = {C}_{2}{e}^{αx} + {D}_{
2}{e}^{−αx}.
| (4.7) |
Let us first look at E > 0. In that case the equation in regions I and III can be written as
|
{{d}^{2}\over
d{x}^{2}}ψ(x) = −{2m\over
{ℏ}^{2}} Eψ(x) = −{k}^{2}ψ(x),
| (4.8) |
where
|
k = \sqrt{{2m\over
{ℏ}^{2}} E}.
| (4.9) |
The solution to this equation is a sum of sines and cosines of kx, which cannot be normalised: Write {ψ}_{III}(x) = A\mathop{cos}\nolimits (kx) + B\mathop{sin}\nolimits (kx) (A, B, complex) and calculate the part of the norm originating in region III,
We also find that the energy cannot be less than − {V }_{0}, since we vannot construct a solution for that value of the energy. We thus restrict ourselves to − {V }_{0} < E < 0. We write
|
E = −{{ℏ}^{2}{k}^{2}\over
2m} ,\kern 2.77695pt \kern 2.77695pt \kern 2.77695pt E + {V }_{0} = {{ℏ}^{2}{κ}^{2}\over
2m} .
| (4.11) |
The solutions in the areas I and III are of the form (i = 1,3)
|
ψ(x) = {A}_{i}{e}^{kx} + {B}_{
i}{e}^{−kx}.
| (4.12) |
In region II we have the oscillatory solution
|
ψ(x) = {A}_{2}\mathop{ cos}\nolimits (κx) + {B}_{2}\mathop{ sin}\nolimits (κx).
| (4.13) |
Now we have to impose the conditions on the wave functions we have discussed before, continuity of ψ and its derivatives. Actually we also have to impose normalisability, which means that {B}_{1} = {A}_{3} = 0 (exponentially growing functions can not be normalised). As we shall see we only have solutions at certain energies. Continuity implies that
Tactical approach: We wish to find a relation between k and κ (why?), removing as manby of the constants A and B. The trick is to first find an equation that only contains {A}_{2} and {B}_{2}. To this end we take the ratio of the first and third and second and fourth equation:
We can combine these two equations to a single one by equating the right-hand sides. After deleting the common factor κ, and multiplying with the denominators we find
which simplifies to
|
{A}_{2}{B}_{2} = 0
| (4.17) |
We thus have two families of solutions, those characterised by {B}_{2} = 0 and those that have {A}_{2} = 0.