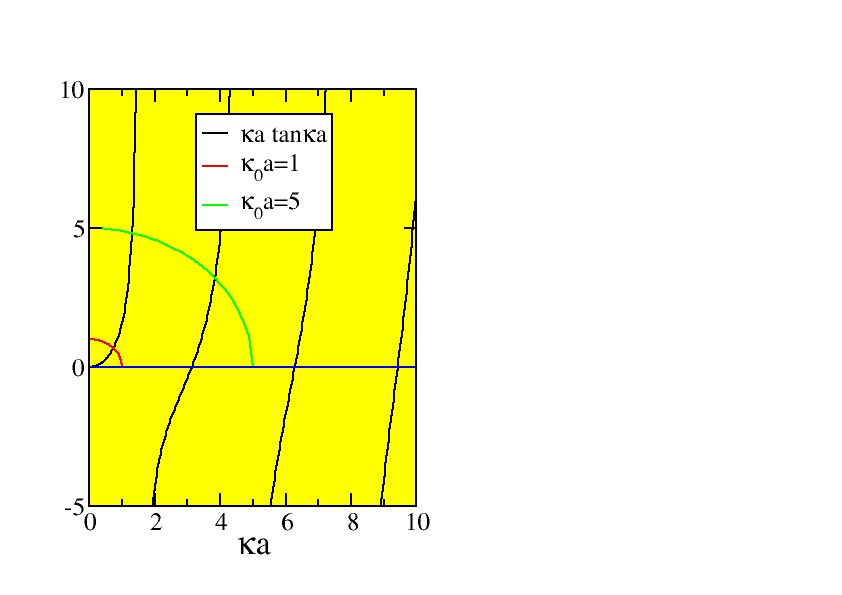
Figure 4.2: The graphical solution for the even states of the square well.
In the first case we read off that {A}_{1} = {B}_{3}, and we find that k and κ are related by
|
ka = κa\mathop{tan}\nolimits κa.
| (4.18) |
This equation can be solved graphically. Use k = \sqrt{−{κ}^{2 } + {κ}_{0 }^{2}}, with {κ}_{0}^{2} = {2m\over {ℏ}^{2}} {V }_{0}, and find that there is always at least one solution of this kind, no matter how small {V }_{0}!
In the middle region all these solutions behave like sines, and you will be asked to show that the solutions are invariant when x goes to − x. (We say that these functions are even.)