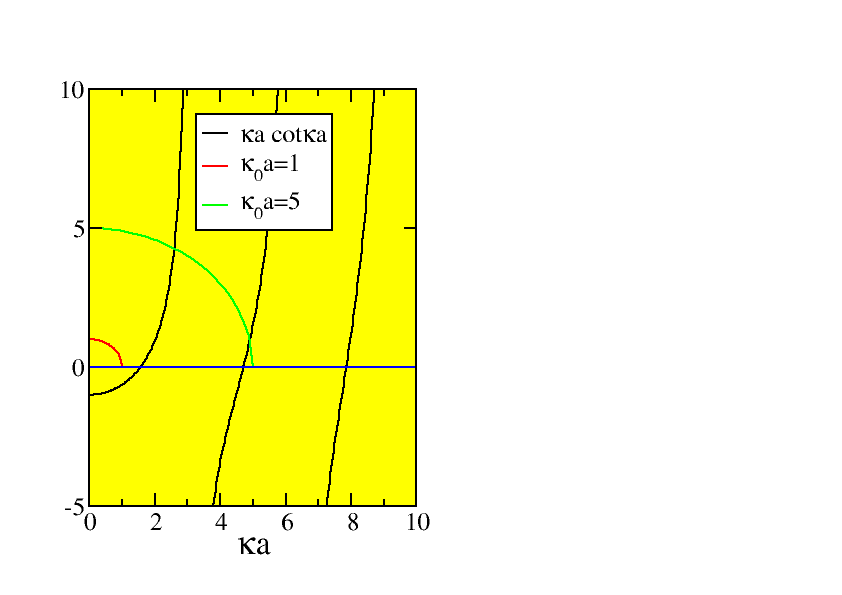
Figure 4.3: The graphical solution for the odd states of the square well.
In this case {A}_{1} = −{B}_{3}, and the relation between k and κ is modified to
|
ka = −κa\mathop{cot}\nolimits κa.
| (4.19) |
From the graphical solution, in Fig. 4.3 we see that this type of solution only occurs for {κ}_{0}a greater than π∕2.
In the middle region all these solutions behave like sines, and you will be asked to show that the solutions turn into minus themselves when x goes to − x. (We say that these functions are odd.)